1Sorry , but that ' s wrong .
Since our exams are approaching fast , I have taken an initiative to post and solve problems that I have found to be quite intriguing . These are all from IIT - JEE syllabus , and I hope to create a field of mutual participation and preparation .
Here goes my first one -
Let " n " be a positive integer . Find the number of polynomials " P ( x ) " with co - efficients in the set S = { 0 , 1 , 2 , 3 } such that " P ( 2 ) = n " .
-
UP 0 DOWN 0 1 15
15 Answers
1i didnt understand some bits of ur question but the concept i am damn sure is right
any polynomial is in the form
of
an2n+an-12n-1..... +a1 2+a0
1st i assuming there r no restricitons menas that coefficients can be repeated
1st case
when
assuming it is a plynomial of only degree 1
then
numbe rof vale taken will be
2+(n-2)
4+(n-4) that is 3 values
6+(n-6)
now for two degree number of values
2+0+(n-2)
2+2+(n-4) so 4 values
2+4+(n-6)
2+6+(n-8)
now the next value will
4+0+(n-4).... 4 values
like this 12 values
now ofr polynomial of 3 degrees is 3*4*4 =48 values
will be 3*4n-1+3*4n-2..... +12+3
thereofre total value if we limit it to a degree of n polynoamials is
4n-1
1coefficiet of xn in the expansion of
\left(1+x+x^2+x^3 \right)(1+x^2+x^4+x^6)....\infty
which does not help as usual !
any other way than multinomial theorem ??
1Way to go Pandit , that ' s the first step . But without using multinomial , we actually can pack this up . I 'll post the detailed solution tomorrow .
1\left(\frac{x^4-1}{x-1} \right)\left( \frac{x^8-1}{x^2-1}\right)\left(\frac{x^{12}-1}{x^4-1} \right)....\infty
u now can see the numerator cancell out leaving
\left(\frac{1}{x-1} \right)\left( \frac{1}{x^2-1}\right)
so you need the coeffiecent of xn in the expansion of \left(\frac{1}{x-1} \right)\left( \frac{1}{x^2-1}\right)
which i guess can be done by partial fraction split followed by series expansion
1\left(\frac{1}{x-1} \right)\left( \frac{1}{x^2-1}\right)=\left(\frac{1}{(x-1)^2} \right)\left( \frac{1}{x+1}\right)=\left(\frac{A}{x-1} \right)+\left(\frac{B}{(x+1)} \right)\left(\frac{Cx+D}{(x-1)^2} \right)
now putting x=0,2,-2,and 3
we end up with four equations to solve for four variables (i.e A,B,C,D)
for that i used http://www.1728.com/unknwn4.htm
and got A=14 ,B=14,C=0 and D=12
so we need to find coefficient of xn in the expansion of
\frac{1}{4}\left(\frac{1}{x-1} \right)+\frac{1}{4}\left(\frac{1}{x+1} \right)+\frac{1}{2}\left(\frac{1}{(x-1)^2} \right)
now using the following expansions
\left(\frac{1}{1-x} \right)=1+x+x^2+x^3+...\infty \\ \left(\frac{1}{1+x} \right)=1-x+x^2-x^3+...\infty \\ \frac{1}{4}\left( \left(\frac{1}{1+x} \right)+\left(\frac{1}{1-x} \right)\right)=\frac{1}{2}(1+x^2+x^4+x^6+...\infty) \\ \frac{1}{(1-x)^2}=1+2x+3x^2+4x^3+..\infty \\ coefficient \ of \ x^n \ in \ \frac{1}{4}\left( \left(\frac{1}{1+x} \right)+\left(\frac{1}{1-x} \right)+\frac{1}{2}\frac{1}{(1-x)^2}\right)=\frac{1}{2}\left(1+(n+1) \right) \ if \ n \ is \ even \\ \ \ \ \ \ \ \ =\frac{n+1}{2} \ if \ n \ is \ odd
341Oh goody! I was trying out something with binary expansion and not getting anywhere :(
1that all is ok but why coeff of xn in \left(1+x+x^2+x^3 \right)(1+x^2+x^4+x^6)....\infty ?
1coeff is 2k can be anything from 0,1,2,3
so that term can be any one of 0, 2k , 2 x 2k
, 3 x 2k
so for
k =0 choices are 0,1,2,3
k=1 0,2,4,6
k=2 0,4,8,12
....
we hav to select one out of 4 frm each set and its um shud be n
so that is coeff of xn in (1+x+x2+x3)(1+x2+x4+x6)(1+x4+x8+x12).......
This is how u shud hav given the solution , so that every 1 can understand
aage solve hojaega u didnt tell the concept itself wich was more imp
NO HARD FEELINGS , CHEERS
1Let us denote the set of required polynomials as " S " .
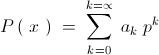
where each " a k E { 0 , 1 , 2 , 3 } " .
Then , each " a k " can be written as , ......... a k = 2 b k + c k
Again , obviously " b k , c k E { 0 , 1 } " .
Now.........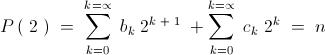 
or....................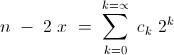 
.....................( 1 )
where ..............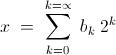 
Obviously , for each " x " which satisfies " 0 ≤ x ≤ [ n2 ] , there is one , and only one way of writing " x " as ,
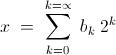....... i . e , an unique way of expressing " x " in base 2 .
Also , from ( 1 ) it must be clear that there are no other ways ; than one and one only to express " n - 2 x " in base 2 .
Hence , we have an intersection between the sets " T = { 0 , 1 , 2 , ...........[ n2 ] } " and the set " S " .
So the number of such polynomials is ................... [ n2 ] + 1 !!!!!!
Voila !!!!!!