1TOTAL RECTANGLES POSSIBLE ON A CHESS BOARD IS 1296.
(13+23+33+.........+83)
AND TOTAL NUMBER OF RECTANGLES EXCLUDING SQUARES ARE 1092.
(Σr3 - Σr2) WHERE r VARIES FROM 1 TO n IN AN nxn SQUARE.
28 Answers
1
1nishant bhaiya if taking rectangle then we have to consider for square(a special case of rectangle)
62hey sorry i missed this one...
Even i din know.. i thought that it was a coincidence.. but then u posted it in the form of sumof cubes.. so i felt if there was somethng good I could learn.... (and bcos u generally give good answers to perm comb questions, i thought abhirup that u had something good to share )
;)
13isn't it just a coincident
n+1C2* n+1C2=[n(n+1)/2]2=Σn3
13no. of rectangles can also be found this way
13+23+33+...+83
i want the logic behind this...actually asked by Nishant bhiyaa.
13Nishant bhiyaa....plz tell us the logic behind putting cubes.....i don't have the ans
13But what about cubes???? i m confused.....getting no logic :(
13yes abhirup... this is an easier way...
if there are n-vertical lines and p-horizantal lines... then
no. of rectangles possible (including squares) = n+1C2 x p+1C2
no. of squares = n.p + (n-1).(p-1) + (n-2).(p-2) + ... (till the product becums zero)...
[1]
13I don't have the logic behind putting cubes....sorry....plz tell us...i want to know it....
Hence i prefer doing it this way 9C2*9C2
i think it's easier to visualize this way
62i am not doubting the validity .. but just for the sake of completion :)
62suraj and abhirup, can u post the method/logic how you got to the figure in terms of cubes?
106are squares counted in rectangles as well??
@ nishant bhaiyya: in exam if we get the same question will we consider the no. of pure rectangles or no. of squares + rectangles
13no. of rectangles can also be found this way
13+23+33+...+83
13anyway the no. of squares are
12+22+32+......+82
1thank u sir i understood ...u mean to say 9 verical n 9 horizontal lines r involved in making the whole chessboard
thank u bhaiya
62in IIT they will never give vague questions..
if by any chance they do.. then you have to pick the answer including the squares...
62
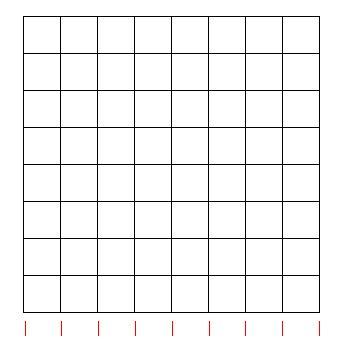
how many red lines are there..
choosing any two lines will fix the two sides of a rectangle...!
62abhinav.. it will be given in the exam.. (if it is not then you have to count squares..)