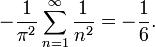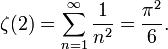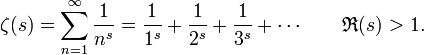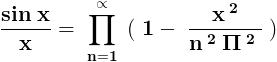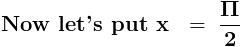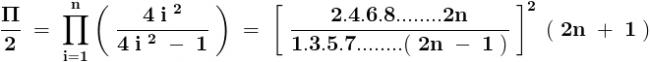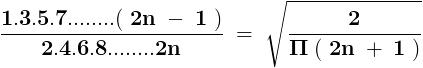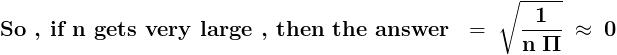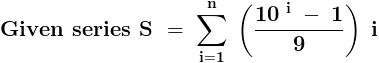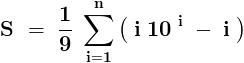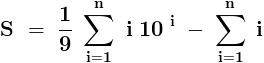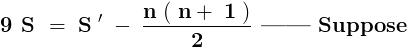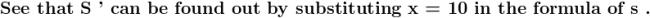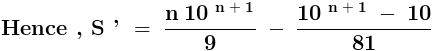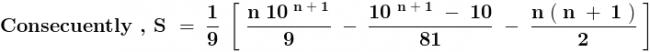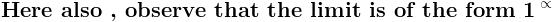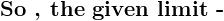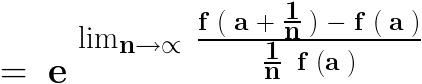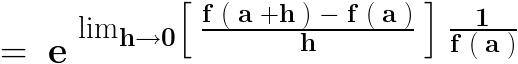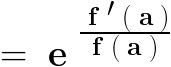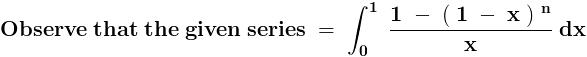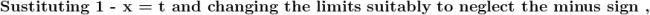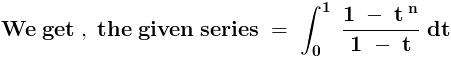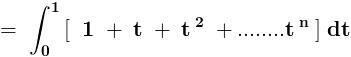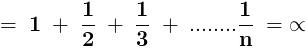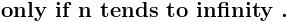sin\,x=2sin\,\frac{x}{2}.cos\,\frac{x}{2}=4sin\,\frac{x}{4}.cos\,\frac{x}{2}.cos\,\frac{x}{4}=8sin\,\frac{x}{8}.cos\,\frac{x}{2}.cos\,\frac{x}{4}.cos\,\frac{x}{8}
continuing for n times we get
sin\,x=2^nsin\,\frac{x}{2^n}.cos\,\frac{x}{2}.cos\,\frac{x}{4}.cos\,\frac{x}{8}.....cos\,\frac{x}{2^n}
let us multiply and divide this product by x and rewrite 2nx.sinx2n as sinx2nx2n
we get,
sin\,x=x\frac{sin\,\frac{x}{2^n}}{\frac{x}{2^n}}.cos\,\frac{x}{2}.cos\,\frac{x}{4}.cos\,\frac{x}{8}.....cos\,\frac{x}{2^n}
now if we let n→∞ by keeping x constant we will get.....
in formlimh→0sin hh=1
thus for infinite terms we get,
\frac{sin\,x}{x}=cos\,\frac{x}{2}.cos\,\frac{x}{4}.cos\,\frac{x}{8}.....\propto
\Rightarrow \frac{sin\,x}{x}=\prod_{1}^{\propto }{cos\frac{x}{2^n}}
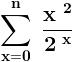
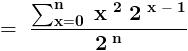

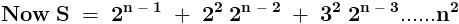
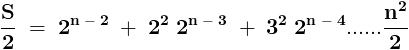
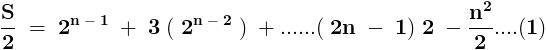
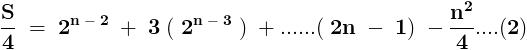
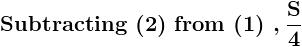
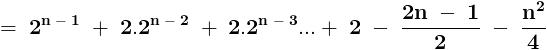
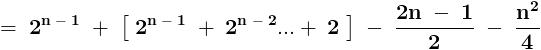
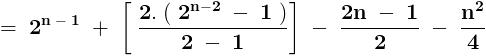
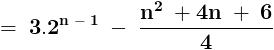
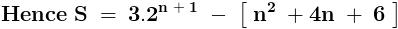
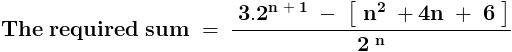
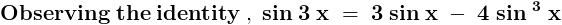
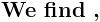
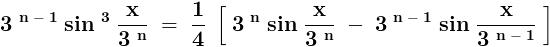
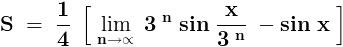
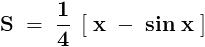
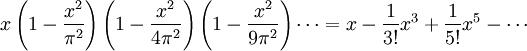 .......... ( 1 )
.......... ( 1 )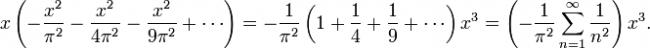 .............. ( 2 )
.............. ( 2 )