24ya u r rite...i too used area...but ans is 1/12
Q1 A point chosen from 1st quadrant x,y ε[0,4] ,the probablity that it satisfies [x]+[y]=3 is ??
I am getting 1/16
Q2 3 points P,Q,R are selected at random from circumference of circle.Find probablity that they lie on semicircle
No idea abt this one
Q3 2 points are taken at random on a given st line AB of length a.Find probablity that the distance b/w them exceeds length c(<a)
No idea abt this one
Q4 2 die thrown simultaneously to get coordinates of a point onXY plane.Find probalbity that this point lies inside lxl+lyl=3
i ma getting 1/8
Q5 Let X={x:1≤x≤50,xεN}.A member of set X is selected at random.Find probablity that it satisfies x2-30x+200x-15<0
I am getting 15/50
Q6 2 nos . λ,μ are chosen one after another at random(with replacement) from set {a:1≤a≤10,aεN}.Find probablity that x2+λx+μ>0 for all xεR
-
UP 0 DOWN 0 1 27
27 Answers
1hey i am right in q-3
i made a silly mistake in case 2
P(x) = \frac{a-(x+c)}{a} . \frac {c}{a} \\ P_{avg} = \frac{2 \int_{0}^{c}{P(x)dx}}{\int_{0}^{c}{dx}} \\ multiplied \ by \ 2 \ coz \ similar \ argument \ can \ be \ made \ from \ end \ \ B \\ \\ now \ add \ two \ cases \ ... \\ we \ will \ get \ \\ P = (\frac{a-c}{a})^2
24ans given by joke is rite....trying to understand it..
anyways thx all....[1]
24@akari, I couldnt understand ur soln2
and btw plz post soln for Q3..
4I was trying to explain in the same way as akari but ya I screwed up the fig a bit
1@akari....yeh kya kiya.....samajh nai aaya....btw is probabilty density fuction in syllab?btw 2nd one was alredy answered by eragon
and @ eureka is my ans for 3rd correct ? if its correct then only i will post teh soln
1the solu tion for 2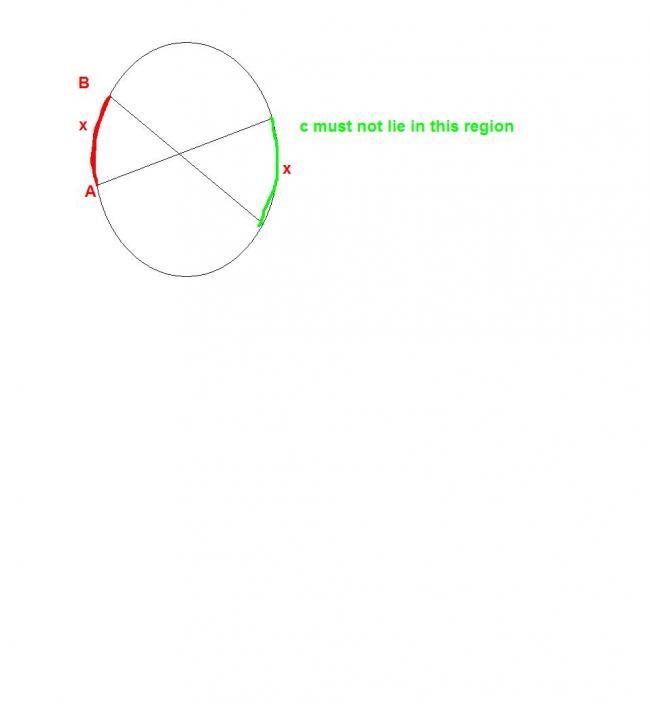
P'(x)=\frac{x}{2\pi r} \\ \\ \ \ P'_{avg} =\frac{\int_{0}^{\pi r}{P'(x).dx}}{\int_{0}^{\pir}{dx}} \\ \\ P'_{avg}_=\frac{1}{4} \\ required \ probablity = 1-\frac{1}{4}
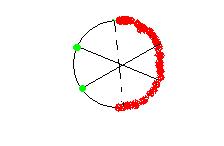
1i hav thought of ques. 2 in a different way
if we fix one point and then vary the other 2 points then in order that the 3 points lie in a semicircle the other 2 points hav to make an angle greater than 90° and less than 180°
and the angle varies from 0° to 180°
so the probability becomes 1/2
i know the ans. is not same as above but wats wrong in this method
24oops.................
so silly mistakes today.,..........
thanks guys......
plz finish Q3 and lets close the thread
14) in this der r 3 points inside lxl+lyl=3 na....(1,1) (2,1) and (1,2)....
so probab 3/36=1/12
41) X ε [0,1) x ε [1,2) x ε [2,3) X ε [3,4)
Y ε [3,4) y ε [2,3) y ε [1,2) Y ε [0,1)
The point shud come under any one of the above 4 combination of cases to satisfy the given condition
total cases = no of mappings from X containing of { [0,1) U [1,2) U [2,3) U [3,4) }
to Y containing of { [0,1) U [1,2) U [2,3) U [3,4) }
= 4C1 x 4 = 16
P = 4/16 = 1/4
44) We can't use area here as it is not a continuous function
No of favourable cases is x=2, y=1 ; x=1 , y=2 ; x=1,y=1
Total cases are 6 x 6
P = 3/36 = 1/12
21
btw i din get any head or tail of wat uttara did
perhaps i guess she was trying to do it with probab density function....though i dun hav any idea of tat
24thx uttara and thejoker,
@joker plz explain ans3
and ans 4 is given 1/12 [2][2]
@uttara i couldn tunderstand ur favourable cases in 2[2]
42) Two points r considered as shown in the fig.
The third point shud be on anywhere on the red coloured arc
If v consider the probabilities the arc length cud b ∩R .... 0
P =2Î R(1/2 + ......+ 3/4 +......0 ) / 2 Î R
= 3/4
(I took avg of the denominator since it's a continuous variation . Even if v integrate v get the same result)
My previous method was wrong since the 2 events i considered were not equally l i k e l y !!
12) 3/4
3)... \left(\frac{a-c}{a} \right)^{2} ???
5)...mine is also 15/50
6) 38/100
46) for x2+λx+μ>0 λ2 - 4μ < 0
λ2 < 4μ
P = 6 + 3(5) + 2(4) + 2(3) + 1(2) + 1/ 10 x 10 = 38/100
45) either x < 10
or
15 < x < 20
P = natural no.s in {[1, 10) + ( 15 , 20)} / 50 = 9 + 4 / 50 = 13/50
24oops..was making sillly mistake in 1)
got hte answer....its 1/4
here is soln if anyone wants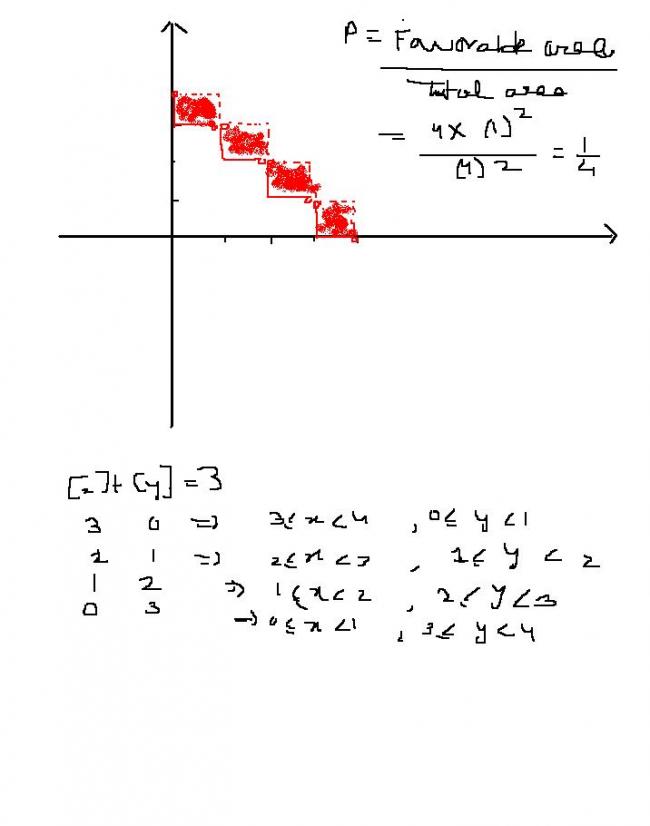
11 st one mine is coming 4/16
(area of the regoin [x]+[y]=3 satisfying the region x,y E [0,4])/(area of the region given by x,y e [0,4])
=4/16