@your time
agree with you
Three numbers are chosen at random from 1 to 20. The probability that they are consecutive is
-
UP 0 DOWN 0 0 47

47 Answers
this is not hit and trail, but is it
13C1/52C1+13C1/52C1
=1/2???
@ronak
the first question's answer you gave is not totally right a slight mistake is there in one term
level THREE
probability=[1/52 * 3/51 +12/52 * 4/51] * 2!
=1/26
[thanx vaibhav u got me a point for noting witht he probability questions in this one!!!!]
ok, ill generalize my question for u guys. this one is good,
we have select m numbers out of the first n natural numbers. find the probability that the m numbers are in a.p for
1) m=3
2) any general m.
this will be a good problem :)
cheers!!
can somebody tell me if my a.p. question's (by gordo) answer is right or not??? i have edited it
gordo i think question needs some more ELABORATION coz u see for n=odd AND n= even different answers are there so one should work separately for ODD number cases [1]
(1/52)*((12/52)+(3/52))*2 + (12/52)*(3/52)*2
=30/52^2 +72/52
plz tell me its correct
ok problem for A.P. done :::::::
CASE-1 : n = odd no.[of form 2k+1 .... k=1,2,3......... REASON TO CHOOSE THIS FORM?????
coz minimum n=3 CHEERS!!!!!!!!!!]
now no. of AP with common difference 1= 2k-1
with c.d. 2 = 2k-3
..............
......
......
no. of AP with c.d. k =1
so, total no. of APs =k2
so probability = k2/ [2k+1 C 3]
=3k/[4k2-1]
so now this was case for ODD no. n ≥3
Personal suggesstion : some one reading it in a alert way should ask me WHERE "k" was given in the ORIGINAL PROBLEM.........n i am asking the same question to GORDOOOOOOO........[unless we put in k in terms of "n"........so wat was the use to ask the problem in that form???.to just make the problem more tedious so tht one should remember to put in "k" in terms of n???]
well for second question for any general "m"=1,.....,n when we go over to find the TOTAL probability u asked us to find...at JEE level the theorem we have wants the condition to be ensured to be E1∩E2∩....∩En=0
and clearly this condition does not hold here........so i think problem is not framed properly!
hey gordo the question that u have made is not appropriate
even if you mention if m=odd or even then too this problem is very complicated and big one if u go on doing it ,it would make number of cases and the no of cases depends upon the value of m . however some cases i can mention here:
m= total no's
n= no's chosen
k=m/2
case I:(works for both odd and even values of m given that n satisfies condition below)
if n >k
P(required)= (1/4)*((m(m+2))/mCn)
case II: (for even no's)
if n=k
P(required)= ((m+4)/mCn)
case III:
for n<k
here is where the problem comes there are no of cases for this individual case
and even if you write all those cases it would make the problem more complicated than if you give data values to m and n. and u know it that for solving probability u never need formulas
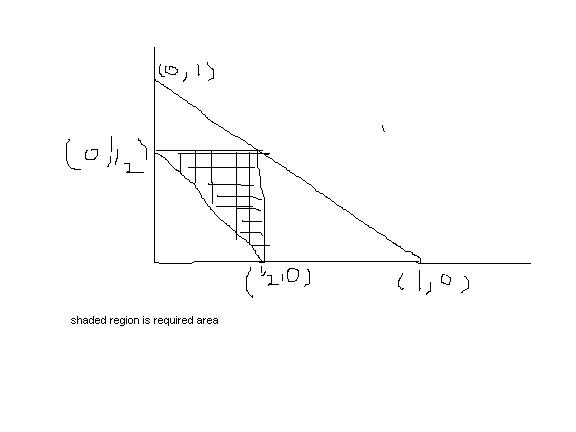
let the length of the first part be 'x' and the second part be 'y', the third part is automatically
l-(x+y)
for obvious reasons we have
x+y≤l (sample space)
it is indicated by the region enclosed by line x+y=l and cordinated axes
if the three pieces have to form a triangle
from triangle inequal;ity we have
x+y≥l2 (required area shadedd in red)
so the P=requiredsample space=area shadedtotal area=34
vaibav's answer is right
i didnt notice that
x+(a-x-y)>y
y<a/2
x<a/2
so the answer is 1/4
A plane is ruled with parallel straight lines at equal distances of 2a.A needle ,2l long (l<a) , is thrown on the plane at random.Find the probability that the needle will hit any of the lines.
Consider a bag containing 10 balls of which few are black. Probability that the bag contains exactly 3 black balls is 0.6 and probability of the bag containing exactly 1 black ball is 0.4. Now ,balls are drawn from the bag, one at a time,without replacement, till all the black balls have been drawn. Find the probability that the procedure will end at the 6th draw.
ab se main koi question try nahin karoonga jao!!!!!! hamesha mujhe pink nahin milta :P :P :P :P :P