39Avik is this theorem of total probability? Jiska bas ek hi question diya hua hai NCERT mein(baaki Bayes theorem par hain)...
(1) A bag contains 4 balls. Two balls are drawn at random and are found to be white. What is the probability that all balls are white?
-
UP 0 DOWN 0 0 20
20 Answers
391@kayamant But, sir, u assumed the probability of having each of the no. of white balls equal(so, each 1/5)
And I assumed that there are 4 balls in a bag and each of them can be either white or non-white.And in this solution also,Ek(1-5) is a set of mutually exclusive(no two combinations match) and mutually exhaustive events(adding Ek(1-5),we get 1).
So, I would really appreciate if u take closer look at my solution and tell if my approach is right.
thanx..
66While applying Baye's theorem one should keep in mind the following. If Ak (k=1,2,..,n) be the set of mutually exclusive and exhaustive events, then the probabilities P(Ak) appearing in the Baye's theorem
P(A_j|A)=\dfrac{P(A_j)P(A|A_j)}{\sum_{k=1}^n P(A_k)P(A|A_k)} for j = 1, 2, ... ,n
are the so called a priori probabilities. That means these are the probabilities of the events Ak without the information supplied by A.
For example, in the given problem, suppose we denote the event
Ak = { the bag contains (k&ndash 1) white balls} for k = 1 to 5
so that we have taken all possible number of white balls in the bag. These five events are equally probable, so that P(Ak) = 1/5.
Suppose the event A = {two white balls are drawn} Then we need P(A5|A)
The denominator appearing in the Baye's theorem is precisely the probability of A as obtained from the theorem on total probability which just asks to take all possibilities. So finding P(A) first we have
P(A) = P(A1)P(A|A1) + P(A2)P(A|A2) + P(A3)P(A|A3) + P(A4)P(A|A4) + P(A5)P(A|A5)
Noting that Ak is the event that the bag contains (k&ndash 1) white balls, the above relation gives
P(A)= 0 + 0 + 15 . 2C24C2 + 15 . 3C24C2 + 15 . 4C24C2 = 13
So finally applying Baye's formula, we get
P(A5|A)= P(A5)P(A|A5)P(A) = 35
which is the required answer. Note that the final result would remain unchanged even if instead of assume 5 cases A1 to A5, we would have assumed only four cases: The bag contains either 1 or 2 or 3 or 4 white balls.
1Let A= Two balls drawn are white
E1 = All 4 balls in the box were white
E2 = 3 white,1 non-white
E3= 2 white,2 white
E4 = 3 non white, 1 white
E5 = All non white
P(E1) = 1/16 (Only 1 combination wwww)
P(E2) = 4/16 (4 combinations wwwn,nwww,wwnw,wnww)
P(E3) = 6/16 (6 combinations,similarly)
P(E4) = 4/16 (4 combinations)
P(E5) = 1/16 (1 combinations)
Now, P(A|E1) = 1
P(A|E2) = 3C2 / 4C2 = 1/2
P(A|E3) = 2C2 / 4C2 = 1/6
P(A|E4) = 0
P(A|E5) = 0
By Baye's Theorem,
P(E1|A) = { P(E1) x P(A|E1) } / {P(E1) x P(A|E1) + P(E2) x P(A|E2) +P(E3) x P(A|E3) + P(E4) x P(A|E4) + P(E5) x P(A|E5) }
= { 1x 1/16 } / { 1/16 + 1/8 + 1/16 + 0 + 0}
= 1/4
So, I think 1/4 is the answer.I am still not sure about this but I dont find any mistake in it.
P.S. Acc. to my solution, this ques does not seem to be of boards level.(Provided this is the intended answer)
Now,@shreyan.. how can one assume equal probability of all the five cases???
@rickde.. the probablity of all the cases can't be same.
@sb... yes there are three possible as the other two (P(A|E4) and P(A|E5) are 0
@avik ... u calculated the probability of getting 2 white balls if there are 3w out of 4 as 3/4 * 2/3 .. vich is correct but that is P(A|E3).Should u not multiply it with P(E3) to apply Baye's theorem?
1already two balls have been drawn, so remaing are two , now prob that both of them are white is 1/2
13Nahi yaar, How can Total Prob. be applied here...? It is Specifically given tht 2Balls have already been drawn & found to be white.
Total ProB. wud have been used if the Qn had been like- "Find the Probability of drawing out 2 White balls frm a bag of 4 unknowns."
.....Tab v wud have taken ProB.(s) of all the possible cases n simply summed up.
1@avik liked how confidently u wrote that[1][1]...3/5sahi hai[1]
but just look at ur ncert text or look below::[1]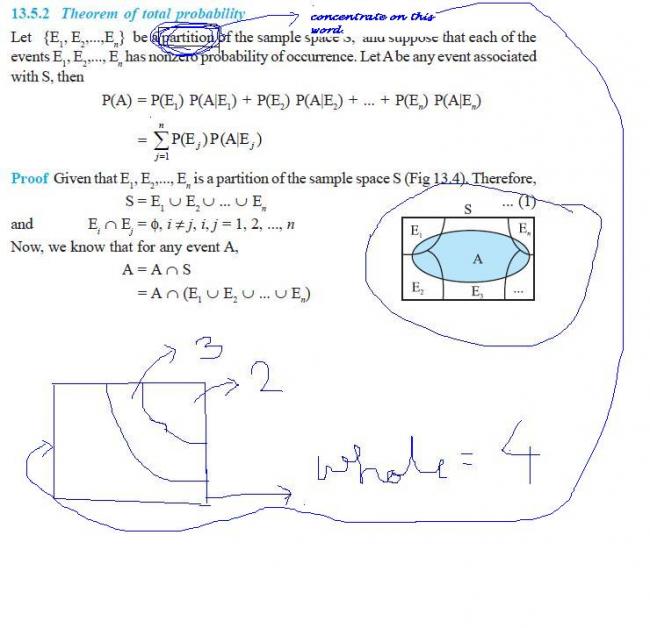
so total probability being applied here........no chance[1][1]..ha!!!!!!ha!!!!!!!!!
11/4??
since v r not concerned with ne colour but white:
so of remaining 3
1w,2w,3w,no-w
since 3w is favourable 1/4
133/5 Sahi hai.
Possible cases-
i)- All WHite, ii)- 3W, iii)- 2W
Probabilities fr drawing 2W successively frm each,
P(i)=1
P(ii)=3/4*2/3
P(iii)=2/4*1/3
Required= P(i)/[P(i)+P(ii)+P(iii)]=3/5
1@subho.......
i appreciate that u showed presence of common sense in ur #6...[1][1][1][1].
maybe i guess cbse wanted to check the commonsense of students......this was not tht tough to be a six mark quest lol!!!!![3][3][3]
1hey if i go by logic n reason it seems a simple 1/4.[simple use of equiprobability theorem [1][1]]
method-2 [by drawing a sample space for remaining four balls n using class-IX probability formulas..lol!!![3][3][3]]
1let Wk denote the event that there are k white balls
A be the event of drawing two white balls from the bag...
we assume P(Wk) = 1/4 for all k 1 - 4
then reqd P(W_4|A)=\frac{1/4}{0+1/4(1/6)+1/4(3/6)+1/4(1)}=\frac{1}{10/6}=\frac{3}{5}
like this perhaps...
49but what i do not understand how 0 balls can be white or 1 ball can be white??
because it is already given that two balls drawn randomly are white.
so the cases must be 2 white balls , 3 white balls , 4 white balls
only these three cases, isn't it??
1arre... i found this ques quite good.....in view of CBSE standards...
i was getting 3/5
take five cases: 0 white balls, 1 white ball, 2 white balls,.....4 white balls. assume equal likelihood of all (1/5)
then apply Bayes' Theorem...
