1I think answers are wanted in terms of x
A random point is unifomly distributed in a square of side length 1 unit.
Q1 Find probablity thta distance of A from nearest side doesnt exceed x (x<1/√2)
Q2 Find probablity thta distance of A from centre does not exceed x (x<1/√2)
Q3 Find probablity thta distance of A from fixed vertex of square does not exceed x(x<√2)
-
UP 0 DOWN 0 1 12
12 Answers
62This i sby taking the area...
For example part 2, the area of all x such that x<1/√2 = pi/2 but this whole area is covered by the square...
answer is 1
Q3, the answer is 1 because the whole square will be taken by the distance √2
Same with question 1..
so all answers are 1
1357Q1
(1-2x)2 for 0<x<1/2
1 for 1/2≤x<1/√2
Is this the answer
24no
plzzzzzzzzzzzzz help..should I post the answer and then everyoen can post the soln ?
11http://www.goiit.com/posts/list/algebra-try-this-909198.htm
This may help.
62see I misread the question grossly... i think soumik's link gives the proof nicely... but still if you want i will post it again...
i solved it using x= in each of these...
so lets see for any arbitrary x...
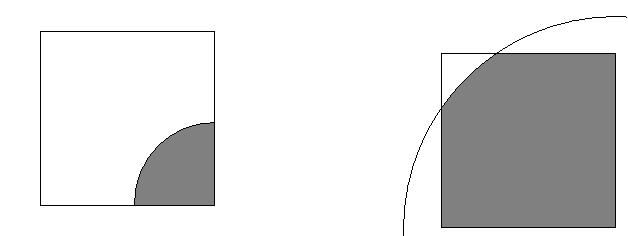
Part 1:
Area of unshaded region is 1-(1-2x)2 which will give the probability...
(I hope i am not overlooking anythign this time :P )
62In the 2nd quesiton there will be 2 cases.. one when radius is less than 1/2
2nd when it will be greater than 1/2 but less than 1/√2
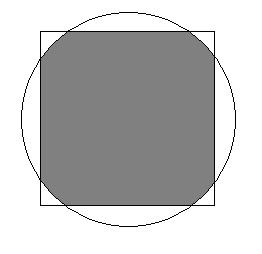
Now use these figures...
24I am giving the answers sir here...now post the soln...
1)4x(1-x)
2)Ï€x2+√4x2-1-4x2tan-1√4x2-1
3)Ï€x24-x2tan-1x2√x2-1+√x2-1
