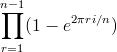12nd question...a bit more interesting :
\sum_{n=1}^{infinity}{} sin nθn
Q1If ω is non real complex cube root of unity tehn find value of
\frac{\prod_{p=1}^{4}{(\omega +\alpha ^p)}}{\prod_{q=1}^{7}{(\omega ^2-\alpha ^q)}}
Q2 If n beolgns to N then value of
\prod_{r=1}^{n-1}{\sin(r\pi /n)}
-
UP 0 DOWN 0 0 6
6 Answers
1
11Ans1) The eqn zn-1 has n roots which are called the nth roots of unity.
Zn = 1 = cos0 + i sin0
= cos 2k∩ + i sin 2k∩
Therefore, Z = cos 2k∩ / n + i sin sin 2k∩ / n where k=0,12,3,......, n-1
Zn-1 = (z-1)(zn-1 + zn-2+ ...........+z+1)
Z n - 1 =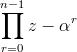 
(zn-1) = (z-1)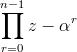
or, (z n-1) / (z-1) = 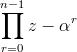..........(1)
Put n=5 and z=-w, then
(-w5-1) / (-w-1) =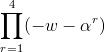 
(w2+1) / (w+1) =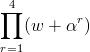 
or -w / -w2 =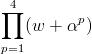
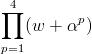= 1/w -------------------(2)
Also in (1), put z=w2, n=8, r=q, then
(w16-1) / (w2-1) =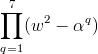 
1 / (w+1) =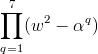
-1/ w2 = 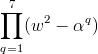.......................(3)
From (2) and (3),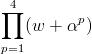 / 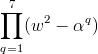= -w
=(1- i √3) / 2
11Z n-1 =(z-1)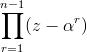 
Z n-1 / (Z-1) =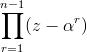
lim z→1 [Z n-1 / (Z-1)] = lim z→1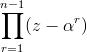
n =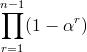 
= 
11CONTINUE....
= 
|n| = 
|n| = 2 n-1 
Therefore, = n / 2 n-1 (bcoz n>1)
