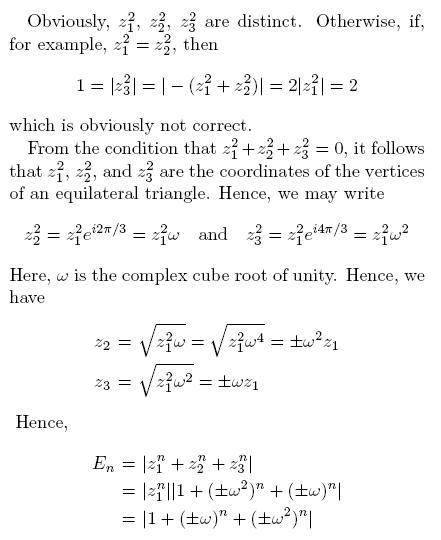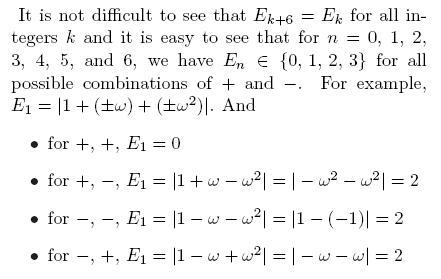1hey wen u try doin
mod of(z1^2+z2^2+z3^2)^2=0
so u get
z1^4+z2^4+z3^4=2Σ(zi^2)(zj^2)...............wer i,j=1,2,3
wich equals 6 ............ and here n=4 wich is>2
so .........................
is ur q wrng or may b ma mistake !
Let z1, z2, z3 be complex numbers such that
1) |z1| = |z2| = |z3| = 1,
2) z1 + z2 + z3 is not equal to zero, and
3) z12 + z22 + z32 = 0.
Then, prove that for all integers n >= 2, the quantity
|z1n + z2n + z3n | is either 0, or 1, or 2, or 3.
-
UP 0 DOWN 0 1 9
9 Answers
62phew.. this is not an easy problem to say the least...
try reducing this problem to a 2 variable structure.. (where does this strike from?) this comes from the fact that all equations are homogeneous)
So u should first try to bring down one variable of the problem by dividing the whole thing by z1
Then give it a shot... it becomes easier.. but still work needs to be done!
1
1357let z1=eiθ
As we have z12+z22+z32=0
we can say that they are the vertices of equilateral triangle.
so we have z12=ei2θ, z22=ei(2θ+120), z32=ei(2θ+240)
or z1=eiθ, z2=ei(θ+60), z3=ei(θ+120)
z'=z1n+z2n+z3n=einθ(1+ei60n+ei120n)
|z'|=|einθ(1+ei60n+ei120n)|=|1+ei60n+ei120n|
see if this can lead you anywhere
11Well I'v managed something to chew upon.....(But not the full soln...)
z1=eia
z2=eib
z3=eic
From given condition....cos2a+cos2b+cos2c=sin2a+sin2b+sin2c=0
cot(a+b)=cot2c
cot(b+c)=cot2a
cot(a+c)=cot2b
a+b=pπ+2c
a+c=mπ+2b
b+c=rπ+2a....adding all 3, we get p+m+r=0......(1)
|zn1+z2n+z3n|2=3+2(cos(na-nb)+cos(nb-nc)+cos(na-nc))
Each (na-nb0, (na-nc), (nb-nc) are of the form π3g, where g is any integer....[88]
Also cos(na-nb), cos(nb-nc0, cos(na-nc) can take any one of the following values only
±12, ±1......
CAN SOMEONE COMPLETE THE REST?
1357continuing further
|z'|=|1+ei60n+ei120n|
=|1+cos(nπ/3)+cos(2nπ/3)+i[sin(nπ/3)+sin(2nπ/3)]
|z'|2=1+4cos(nπ/3)+2cos(2nπ/3)=[1+2cos(nπ/3)]2
|z'|=|1+2cos(nπ/3)|
For n=2 |z'|=0
n=3, it is 1
n=4, it is 0
n=5 it is 2
n=6 it is 3
n=7 it is 2
it repeats further
66Alternately, one may proceed as follows: Let
a=z_1+z_2+z_3
b=z_1z_2+z_2z_3+z_3z_1 and
c=z_1z_2z_3
Then z1, z2, z3 are the roots of the equation
t^3-at^2+bt-c=0 ------(1)
Since z_1^2+z_2^2+z_3^2=0, we get a^2=2b. Also,
z_1z_2+z_2z_3+z_3z_1=z_1z_2z_3\left(\dfrac{1}{z_1}+\dfrac{1}{z_2}+\dfrac{1}{z_3}\right)
But since |z_i|=1, we get
\dfrac{1}{z_i}=\overline{z}_i, and so
z_1z_2+z_2z_3+z_3z_1=z_1z_2z_3(\overline{z}_1+\overline{z}_2+\overline{z}_3) = z_1z_2z_3(\overline{z_1+z_2+z_3})
That is b=c\,\overline{a}
Hence, we get a^2=2b=2c\,\overline{a}
And so |a|^2=2|c|\,|\overline{a}|=2|a|
Since, |a|\neq 0, we get |a|=2.
Let a=2x were |x|=1. Then b=\dfrac{a^2}{2}=2x^2 and c=\dfrac{b}{\overline{a}}=\dfrac{2x^2}{2\overline{x}}=x^3
Hence, equation (1) reduces to
t^3-2xt^2+2x^2t-x^3=0
Factoring this becomes
(t-x)(t^2-xt+x^2)=0
Hence the roots are t=x,\,\omega x,\,-\omega^2x
where \omega = \dfrac{1}{2}+i\,\dfrac{\sqrt{3}}{2}
Let
z_1=x,\ z_2=\omega x,\ z_3=-\omega^2 x
Hence,
S_n=|z_1^n+ z_2^n+z_3^n|=|x^n + x^n\omega^n +(-1)^n\omega^{2n}x^n|=|x^n||1 + \omega^n +(-1)^n\omega^{2n}|
But since |x|=1, we get
S_n=|1 + \omega^n +(-1)^n\omega^{2n}|
Notice that \omega^2-\omega+1=0 and \omega^3=-1. As such
S_n =S_{n+6}
Besides,
S_0=3,\ S_1=2,\ S_2=0, \ S_3=1,\ S_4=0,\ S_5=2
And hence, for all natural n, we get
S_n=|z_1^n+z_2^n+z_3^n|\in\{0,\,1,\,2,\,3\}
341http://www.goiit.com/posts/list/algebra-still-another-one-on-complex-numbers-76576.htm
66Yes that was one of my earlier posts in goiit. There I gave the following (a bit geometrical) solution:
