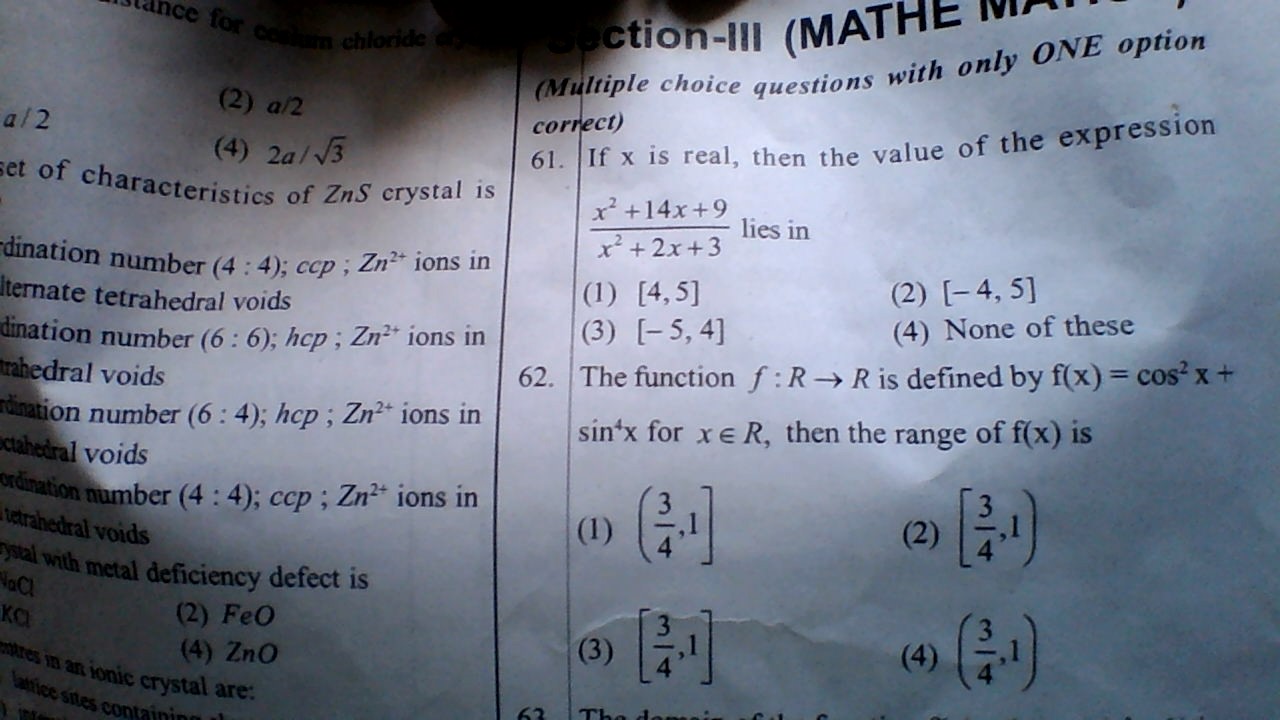1708\hspace{-20}\bf{(62)::\;\;}$ Let $\bf{y=\cos^2 x+\sin^4 x\leq \cos^2 x+\sin^2 x=1}$\\\\\\ So Max. value of $\bf{y=\cos^2 x+\sin^4 x = 1}$\\\\\\ Now for calculation of Minimum....\\\\\\ $\bf{y=1-\sin^2x+\sin^4 x=\left(\sin^2 x-\frac{1}{2}\right)^2+\frac{3}{4}\geq \frac{3}{4}}$\\\\\\ So Min. value of $\bf{y=\cos^2x +\sin^4 x= \frac{3}{4}}$\\\\\\ So range of $\bf{y = f(x)=\cos^2 x=\sin^4 x}$ is $\bf{y\in \left[\frac{3}{4}\;,1\right]}$