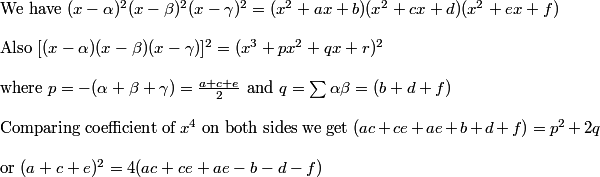Quadratic Equations

\hspace{-16}$Let $\bf{\alpha,\beta}$ be the roots of the equation $\bf{x^2+ax+b=0}$\\\\\\ Then $\bf{\alpha+\beta = -a............(1)}$ and $\bf{\alpha\cdot \beta = b.................(2)}$\\\\\\ Similarly let $\bf{\beta,\gamma}$ be the roots of the equation $\bf{x^2+cx+d=0}$\\\\\\ Then $\bf{\beta+\gamma = -c.............(3)}$ and $\bf{\beta \cdot \gamma = b................(4)}$\\\\\\ Similarly let $\bf{\gamma,\alpha}$ be the roots of the equation $\bf{x^2+ex+f=0}$\\\\\\ Then $\bf{\gamma+\alpha = -e.............(5)}$ and $\bf{\gamma \cdot \alpha = f................(6)}$\\\\\\ Now $\bf{L.H.S}$ is $\bf{\left(a+c+e\right)^2 = \left(-\alpha -\beta-\beta-\gamma-\gamma-\alpha\right)}$\\\\\\ From $\bf{(1)\;,(3)\;,(5)............}$\\\\\\ $\bf{=4\cdot \left(-\alpha-\beta-\gamma\right)^2 = 4\cdot \left(\alpha+\beta+\gamma\right)^2}$\\\\\\ Now $\bf{R.H.S}$ is $\bf{ = 4\cdot \left(ac+ce+ea-b-d-f\right)}$\\\\\\

\hspace{-16}$\bf{=4\cdot \left\{\left(\alpha+\beta\right)\cdot \left(\beta+\gamma\right)+\left(\beta+\gamma\right)\cdot \left(\gamma+\alpha\right)+\left(\gamma+\alpha\right)\cdot \left(\alpha+\beta\right)-\alpha\cdot \beta-\beta\cdot \gamma-\gamma\cdot \alpha\right\}}$\\\\\\ $from equation $\bf{(1)\;,(3)\;,(5)}$ and $\bf{(2)\;,(4)\;,(6)}$\\\\\\$\bf{=4\cdot \left\{\alpha\beta+\beta^2+\alpha\gamma+\beta\gamma+\beta\gamma+\gamma^2+\alpha\beta+\alpha\gamma+\alpha\gamma+\alpha^2+\beta\gamma+\alpha\beta-\alpha\beta-\beta\gamma-\gamma\alpha \right\}}$\\\\\\ $\bf{=4\cdot \left(\alpha^2+\beta^2+\gamma^2+2\alpha\beta+2\beta\gamma+2\gamma\alpha\right)}$\\\\\\ $\bf{=4\cdot \left(\alpha+\beta+\gamma\right)^2}$\\\\\\ So $\bf{L.H.S = R.H.S}$