how would u do it for α9+β9
1. If α,β are the roots of x2+px+q=0 then express α5+β5 in terms of p and q.
2. \left|\left|x-1 \right|-x \right| \leq 4
-
UP 0 DOWN 0 0 8

8 Answers
\mathbf{\alpha^9+\beta^9=(\alpha^3)^3+(\beta^3)^3=\left(\alpha^3+\beta^3\right)^3-3.\alpha^3.\beta^3\left(\alpha^3+\beta^3\right)}$\\\\ $\mathbf{=\left\{(\alpha+\beta)^3-3\alpha.\beta(\alpha+\beta)\right\}-3(\alpha.\beta)^3.\left\{(\alpha+\beta)^3-3\alpha.\beta(\alpha+\beta)\right\}}$
Is there any standard way for solving these type of questions of αn+βn
$\textbf{For Second $\mathbf{x\geq-\frac{3}{2}\Leftrightarrow x\in\left\[\frac{-3}{2},\infty \right\)$}}$
2. case 1
lets consider x as +ve
so, |x|=x
|x-1-x|≤4
it has no solution...............
case 2
lets consider x as -ve
so, |x|=-x
|-x-1-x|≤4
0r, |1-2x|≤4
now,
case 1 under case 2
let 1-2x≥0
so, 1-2x≤4
or, 2x-1≥4
or, x≥5/2
case 2 under case 2
let 1-2x<0
so, 2x-1≤4
or, x≤5/2
the ans is x either ≥2.5 or ≤2.5
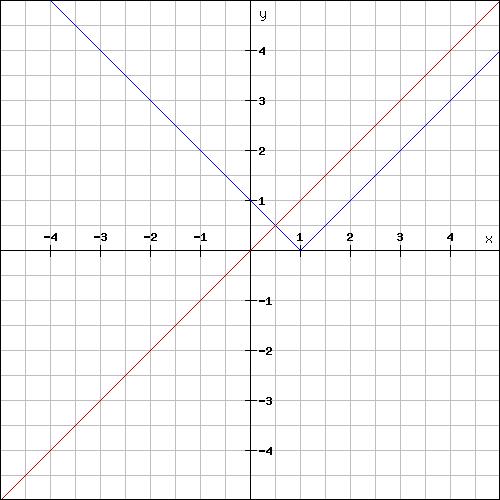
From the graph, it is obvious that the answer is x>=-1.5
*I have used a graph plotter but used it only to plot the most elementary graphs ... of |x-1| and of x... I hpe you all dont try and use graph plotters as far as possible...