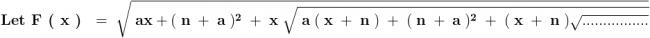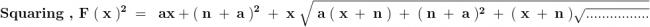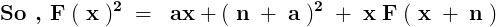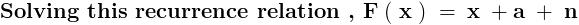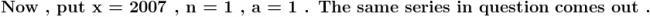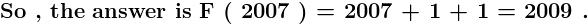1
evaluate-
\sqrt{2011+2007\sqrt{2012+2008\sqrt{2013+2009\sqrt{2014+.........\infty}}}}
-
UP 0 DOWN 0 2 8
8 Answers
1you can take A=2011+2007 then subsequently other will be A+2 and so on
√A√A+2√A+4√A+6...∞
if anyone knows how to solve this further can do it
but i dont know if this method is correct or not....
1ya as prophet sir said its generalisation of Ramanujan's problem.
actually prob which ramanujan posted in Journal of Indian Mathematical Society was this
a variant of prob asked
but no one cud solve it in stipulated time of six months !
then he only gave teh soln.
1Solution of f ( x ) ---
1 > Observe that , f ( x ) must be a polynomial of first degree , as in other cases , the powers of x
in f ( x ) won't match on L . H . S and on R . H . S .
So , f ( x ) = c x + b
Again , f ( 0 ) = n + a
So , b = n + a
So , f ( x ) = c x + n + a .
Now , plug this f ( x ) in the recurrence relation , from where c comes out to be 1 .