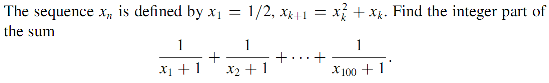Sequences

x_k+1 = x_k(x_k+1)

1x_k+1 = 1x_k(x_k+1) = 1x_k - 1x_k+1

or,1x_k+1 = 1x_k - 1x_k+1

The required sum is =

1x₁+1 + 1x₂+1 + 1x₃+1 + ..........+1x₁₀₀+1
= 1x₁-1x₂+........+1x₉₉-1x₁₀₀
=1x₁ - 1x₁₀₀

x₃ >1
If x_k >1 then x_k+1 = x_k(x_k+1)>1

Using induction we can say that x₁₀₀ >1

Therefore required sum = 1x₁ - 1x₁₀₀ = 2 - 1x₁₀₀.

Since x₁₀₀ >1 , 1x₁₀₀<1

Therefore the integer part of the sum is = 1.