its (pi)2/6
7 Answers
Could we do this by limit of a sum?
\lim_{n\to\infty}\sum_{i = 1}^{n}{\frac{1}{i^2}}
Okay sandi has got it lol.
w8 giving you some links...this sum had created a hell lot of problems...so just remembered the result....
1) http://www.targetiit.com/iit-jee-forum/posts/binomial-theorem-15602.html
(#7 , #9 , #11 , )
2)just quoting #11
"thats a basel problem solved by great mathematicians like euler see this
http://en.wikipedia.org/wiki/Basel_problem
but n must go to infinity
dont ever try to telescope it
many infinitely more brilliant ppl than us are trying for the past seversl thousand years
so telescoping is not possible"
so after this the only way out for me was to just remember the result...
ur answer to the sum of squares od reciprocals of odd terms...
see from above
112 + 122 + 132 + ...... = (pi)26
also
112 - 122 + 132 -......... = (pi)212 (i learnt it as a fact..)
so adding both series we get....
2(112 + 132 + ...) = 3 (pi)2 12
so 112 + 132 + ... = (pi)2 8
[1][1][1]
An alternative:
We start by proving two results, seemingly unrelated to the given problem:
1) \sum_{k=1}^n \cot^2\left(\frac{k\pi}{2n+1}\right) = \frac{n(2n-1)}{3}
2) \sum_{k=1}^n \csc^2\left(\frac{k\pi}{2n+1}\right) = \frac{2n(n+1)}{3}
The second one can be proved from the first one by using the identity \csc^2\varphi = \cot^2 \varphi + 1, so I prove only the first one.
Using De' Moivre's formula, we have
\cos n\varphi + i \sin n\varphi = (\cos\varphi + i \sin\varphi)^n
Expand the right-side binomially:
(\cos\varphi + i \sin\varphi)^n = \sum_{r=0}^n\, ^nC_r i^r \cos^{n-r}\varphi \ \sin^r\varphi
On the RHS, for each even value of r the summand is purely real, while for each odd value of r, it odd. Taking this fact into account and collecting the real and imaginary quantities, we obtain
\cos n \varphi + i \sin n\varphi = (\cos^n\varphi - \, ^n\!C_2 \cos^{n-2}\varphi \sin^2\varphi +\, ^n\!C_4 \cos^{n-4}\varphi \sin^4\varphi - \ldots)
+i\ (\,^nC_1 \cos^{n-1}\varphi \sin \varphi - \,^n\!C_3 \cos^{n-3}\varphi \sin^3\varphi +\, ^n\!C_5 \cos^{n-5}\varphi \sin^5\varphi - \ldots)
Equating the imaginary parts we obtain,
\sin n\varphi = \,^n\!C_1 \cos^{n-1}\varphi \sin \varphi - ^n\!C_3 \cos^{n-3}\varphi \sin^3\varphi +\, ^n\!C_5 \cos^{n-5}\varphi \sin^5\varphi - \ldots
Replacing n by 2n+1, write the above equality as
\sin(2n+1)\varphi =\, ^{2n+1}C_1 \cos^{2n}\varphi \sin\varphi -\, ^{2n+1}C_3 \cos^{2n-2}\varphi \sin^3\varphi +\, ^{2n+1}C_5 \cos^{2n-4}\varphi \sin^5\varphi + \ldots
\Rightarrow\sin(2n+1)\varphi =\sin^{2n+1}\varphi (\, ^{2n+1}C_1 \cot^{2n}\varphi -\, ^{2n+1}C_3 \cot^{2n-2}\varphi +\, ^{2n+1}C_5 \cot^{2n-4}\varphi + \ldots )\qquad (1)
Now, if we take
\varphi = \frac{k\pi}{2n+1},\, k =1,\,2,\,3,\,\ldots,\,n,
then for each of these values, the LHS of the above equation is zero. But since for these values of φ, sin φ is not zero, the quantity inside the bracket must be zero for these values of φ . That means the numbers
x_k = \cot^2\left(\frac{k\pi}{2n+1}\right),\, k =1,\,2,\,3,\,\ldots,\,n
must be the roots of the -th degree polynomial equation
^{2n+1}C_1 x^n -\, ^{2n+1}C_3 x^2 + \,^{2n+1}C_5 x^3 - \ldots =0
As such the sum of the roots of this equation
\boxed{\sum_{k=1}^n \cot^2\left(\frac{k\pi}{2n+1}\right) = \dfrac{^{2n+1}C_3}{^{2n+1}C_1}=\dfrac{n(2n-1)}{3}}
proving the proposition 1) above. As said already, 2) can be obtained from 1), so I do not prove the second one.
Next, it is easy to prove that for a non-zero acute angle (in radians), the following double inequality holds:
\sin\alpha < \alpha < \tan\alpha
(Can someone prove it ? )
From this, we obtain the inequalities
\cot^2\alpha < \left(\frac{1}{\alpha}\right)^2 < \csc^2\alpha\qquad (2)
Hence, we obtain the following sequence of double inequalities:
\cot^2\left(\frac{k\pi}{2n+1} \right)< \left(\frac{2n+1}{k\pi}\right)^2 < \csc^2\left(\frac{k\pi}{2n+1}\right),\,k=1,\,2,\,3,\,\ldots,\,n.
Summing them up and using 1) and 2) already derived, we get
\dfrac{n(2n-1)}{3} < \sum_{k=1}^n \left(\frac{2n+1}{k\pi}\right)^2 < \dfrac{2n(n+1)}{3}
From which we obtain
\dfrac{n(2n-1)}{3}\cdot \dfrac{\pi^2}{(2n+1)^2} < \sum_{k=1}^n \dfrac{1}{k^2} < \dfrac{2n(n+1)}{3}\cdot \dfrac{\pi^2}{(2n+1)^2}\qquad (3)
The left side is
\dfrac{2n}{2n+1}\cdot \dfrac{2n-1}{2n+1}\cdot \dfrac{\pi^2}{6}=\left(1-\dfrac{1}{2n+1}\right)\left(1-\dfrac{2}{2n+1}\right)\dfrac{\pi^2}{6}
while the right side is
\dfrac{2n}{2n+1}\cdot \dfrac{2n+2}{2n+1}\cdot \dfrac{\pi^2}{6}=\left(1-\dfrac{1}{2n+1}\right)\left(1+\dfrac{1}{2n+1}\right)\dfrac{\pi^2}{6}
Hence, from , we obtain the following inequality:
\boxed{\left(1-\dfrac{1}{2n+1}\right)\left(1-\dfrac{2}{2n+1}\right)\dfrac{\pi^2}{6} < \sum_{k=1}^n \dfrac{1}{k^2} < \left(1-\dfrac{1}{2n+1}\right)\left(1+\dfrac{1}{2n+1}\right)\dfrac{\pi^2}{6}}
Taking the limit as n→∞ and applying Squeeze theorem, we get:
\sum_{k=0}^\infty \dfrac{1}{k^2} =\dfrac{\pi^2}{6}
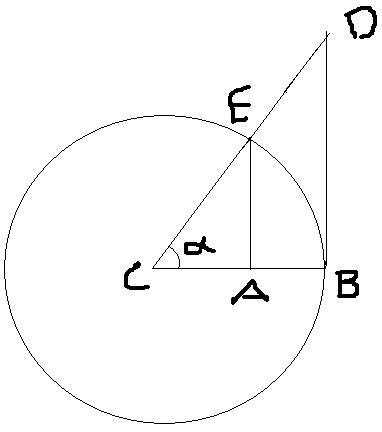
Let us consider a circle of unit radius.
so sin (alpha) = AECE = AE
arc BE = 1.(alpha) = alpha
and tan (alpha) = BDBC = BD
now AE < arc BE < BD
so sin (alpha) < (alpha) < tan (alpha)
