Let f(x) = [3+4Sinx] (where [] denotes greatest integer).
Then, find the sum of all the values of "x" in [Ï€ ,2Ï€] where f(x) fails to be differenciable.....
Answer : 12Ï€
1[] function is non-diff. in integers.
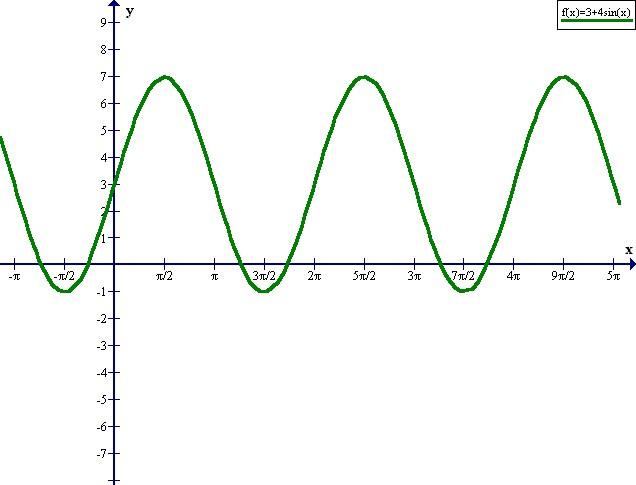
here, f(x) is non-diff. when 3+4sinx becums integer.
possible values of sinx for which the exp. is integer when x≡[π,2π] are
sinx= 0, -1/4, -1/2 , -3/4 , -1 , -3/4 , -1/2 , -1/4 , 0.
x= π, sin-1(-1/4), ..........
likewise find the sum.
sin-1(-1/4) can be taken as π+x .......then its other pair will be 2π-x
adding......Ï€+x+2Ï€-x = 3Ï€
so these pair will give sum together 3Ï€
so sum of all the vaues of x is= 4*3Ï€+ sin-1(-1) =12Ï€+3Ï€/2 = 27Ï€/2
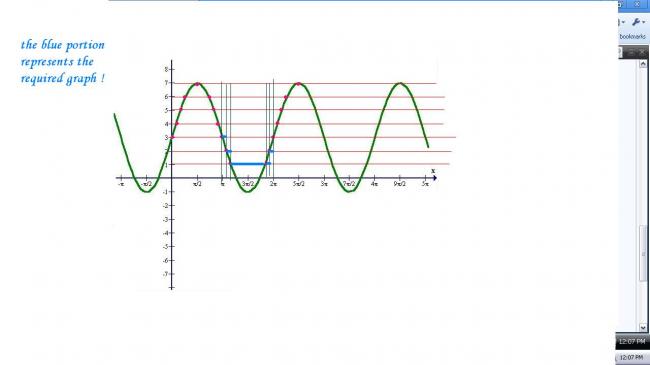
19draw the graph..its mighty useful here ! first draw 3+4sin x...then transform it to [] form i.e. from f(x) to [f(x)] as per the rules of transformation,,,,you will easily get the non diff pts !
1Wait till tomorrow morning...got the answer, will post it
Mujhe bhi neend aa rahi hai[4]
1but if the answer is 12Ï€ then what about the sin-1(-1) term???.........x corresponding to this is 3Ï€/2 & 3+4sinx will be integer too . expert help needed
13Yeah, same doubt as biswajit...
Plz See where am i going wrong....
For func.n to be non-diff., [Z] → Z shud be an integer.
Possible in the given Domain when , Cases for Z →
0 => sum =3Ï€
-1 => Sum = 3Ï€/2,
1 => sum =3Ï€
2=>sum= 3Ï€ ,,,
3 =>sum = 3Ï€
So ans shud be - 12Ï€+3Ï€/2
106Biswajit's solution is perfect except for the fact that the function IS differentiable when x=3pi/2 .. so subtract that... the answer is indeed 12pi
