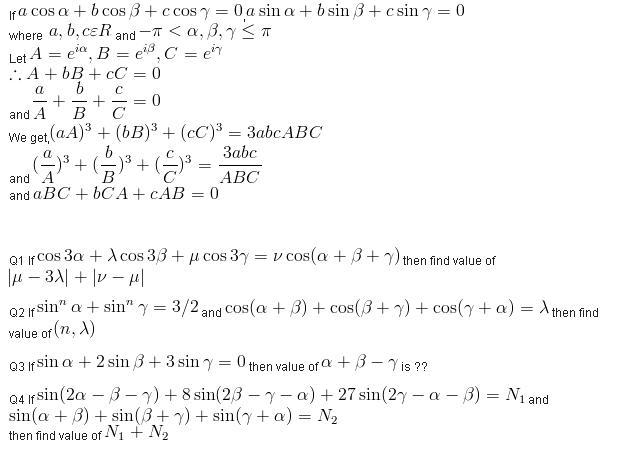62Eureka multiply the 2nd by i and add to the first equation ... you will realize taht
aA+bB+cC = a(cos α + i sin α) + b(cos β + i sin β) + c(cos γ+ i sin γ)
again multiply the 2nd eqtn by i and substract from the first, you will get
a/A+b/B+c/C = a(cos α - i sin α) + b(cos β - i sin β) + c(cos γ - i sin γ)
the 3rd one comes from x+y+z=0 => x3+y3+z3=3xyz
I hope now it has started to look simpler to you :)
11Ans1) (aA)3 + (bB)3 + (cC)3 = 3abc ABC .................(given)
Also it is given that A = e i α B = e i β C = e i γ
Putting these values in the above eqn
a 3 e 3 i α + b 3 e 3 i β + c 3 e i 3 γ = 3abc e i ( α + β + γ) ...................(1)
we know that e i θ = cos θ + i sin θ
Putting in (1) and then comparing the real parts
a 3 cos 3 α + b 3 cos 3 β + c 3 cos 3 γ = 3abc cos (α + β + γ)
Therefore, we get a3 =1 , b3 = λ , c3 = µ , 3abc = v
Therefore,
|µ - 3 λ | + | v - µ | = |c3-3b3 | + | 3abc- c3|
= |c3 - 3b3 | + | 3bc - c3| (bcoz a=1)
24I am writing answers for everyone...plz try them
1) 12
2) (2,3)
3) -2γ
4) 0
24
eureka123
·2009-09-30 01:09:58
IS this impossible question ???????????????????????????????????????
1i think there is some mistake in Q2
it should be sinnα+sinnβ+sinnγ=3/2
taking this
since cos(α+β)+cos(γ+β)+cos(α+γ)=λ
now since aBC + bCA + cAB=0
for a=b=c=1
BC+AB+CA=0
i.e cos(α+β)+cos(γ+β)+cos(α+γ)=0
therefore λ=0
now aA+bB+cC=0 and a/A+b/B+c/C=0
for a=b=c=1
A+B+C=0 and 1/A+1/B+1/C=0
cosα+cosβ+cosγ=0 and sinα+sinβ+sinγ=0
now A2+B2+C2=(A+B+C)2 - 2(BA+BC+CA)
A2+B2+C2=0
cos 2α+cos2β+cos2γ=0
1-2sin2α + 1-2sin2β + 1-2sin2γ=0
sin2α + sin2β + sin2γ=3/2
comparing n=2
therefore ans (2,0)
1
decoder
·2009-09-30 07:02:59
plz check the ans .......it is coming (2,0) not (2,3)
