1.Two circles are constructed taking two sides of a triangle as diameter. What is the probability that these two circles intersect on third side of triangle?
2.In a MAMCQ test, der r 4 alternatives out of which 1 or more r correct.A candidate gets marks if he ticks all the correct answers. The candidate decided to tick randomly.If he is allowed to do 3 attempts, wats the probability dat he gets marks.
Just post the answers, i've solved them.(if possible post the method too, so dat others can see)
1The rod is cut as shown
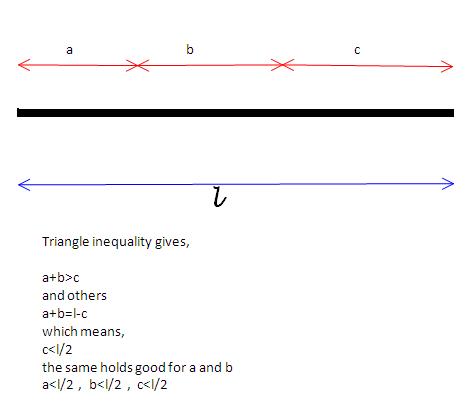
It forms a triangle iff, the above condition is satisfied
Can some1 extend this to probability of being cut to length less than l/2???
624. Two points r selected at random on a straight line of length 10m. Wats prob. that distance between them is less than or equal to 2m?
a, b are two points
we have to find that
|a-b| < 2
we know that 0<a<10
and 0<b<10
so draw the square.. find the probability of the strip on the diagonal...
the answer should be 1-.92 = .19. .. (Did mentally so see any calculation mistake)
623. If n positive integers r taken at random and multiplied together, wats probability dat last digit is 5?
last digit is 5 if atleast one of the numbers is 5 and all numbers are odd
so (5/10)r - (4/10)r
1Sure....
3. If n positive integers r taken at random and multiplied together, wats probability dat last digit is 5?
4. Two points r selected at random on a straight line of length 10m. Wats prob. that distance between them is less than or equal to 2m?
5. A rod breaks into 3 parts. wats the prob. that a triangle is formed?
(i didnt get the exact meaning of this ques and dont even have the answer)
1Could U post more questions of this sort on this thread???
They R simple but striking......
1The probability is 1
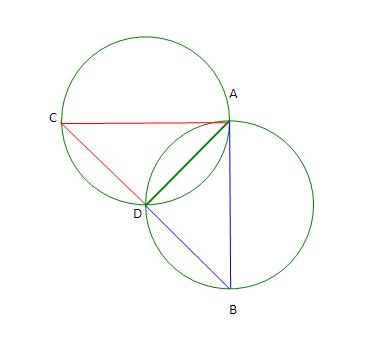
From the figure,
<ADC=900 (angle by diameter)
<ADB=900 (angle by diameter)
Adding,
<CDB=1800
So it is a straight line.
So the Circles always intersect on the line joining BC.
Hence, Probability is 1
[339]
1
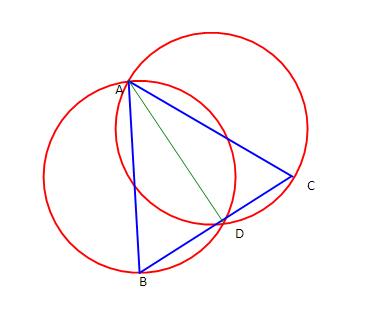
From the figure,
They intersect on third side when
<ADB=<ADC=900
Could sum1 think further on this???
Ill try dis after finishing dinner
1Well this is another approach...........
Each option may be either right or wrong
ie., on the whole there R 24=16 ways of attempting the question.
But all cant be wrong ,I missed this in#9
So there R 15 ways of attempting, of which only 1 is correct.
So 1/15 ways
3 attempts give 3/15.
1@Subash,
It's not necessary dat only one attempt is rite...the only thing is dat he shud get marks, dats it!
1Subash ur approach is rite...
probability of being correct=1/15
So, if he's given three attempts, prob. of being correct is simply 3*1/15
=1/5.
Hope it's clear!
11even if it is wrong i give my soln check it up
the total number of ways he can choose an answer=4C1+4C2+4C3+4C4
out of these only one is correct
probability of being correct=1/15
''''''''''''''''''''''''''''''''''''wrong=14/15
so ans=(14/15)2(1/15)=196/3375(sorry previous ans wrong)
112nd oone
***196/3375****(even this might be wrong)
the marking doesnt mean it is correct showing edited :P
1W.R.T post#5,
There r not 3 questions but he's given 3 attempts for a single question.
622.In a MAMCQ test, der r 4 alternatives out of which 1 or more r correct.A candidate gets marks if he ticks all the correct answers. The candidate decided to tick randomly.If he is allowed to do 3 attempts, wats the probability dat he gets marks.
1- (1-1/16)3
621.Two circles are constructed taking two sides of a triangle as diameter. What is the probability that these two circles intersect on third side of triangle?
is it zero?!
1at d first look .....A candidate gets marks if he ticks all the correct answers.
so if he gets all right only he gets marks....
the probability dat he gets marks.
so for this.....all must be correct...........since there are three questions...
so 1/4*1/4*1/4
=1/64
