a few problems by goyalji

For third one multiply and divide x^(2n-2).

after multiplying and dividing by x^(2n-2),
I multiplied and divided by cos x. then rearranging, I got,

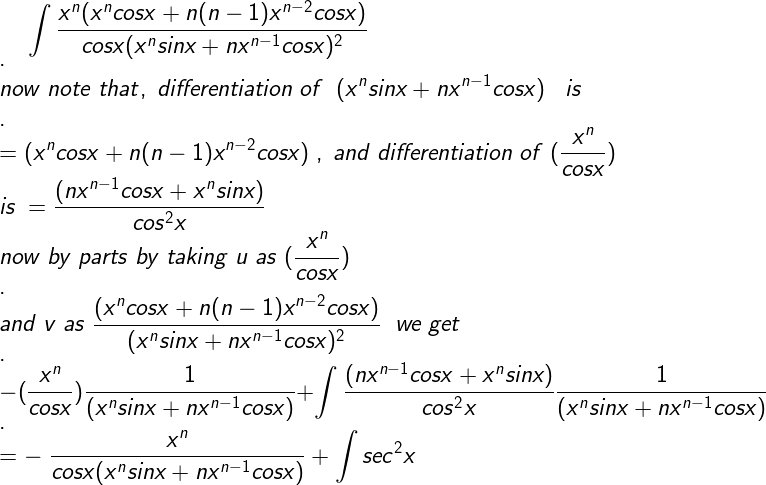
\hspace{-16}\bf{(3)\;::\; }$Given $\bf{\int\frac{x^2+n(n-1)}{\left(x\cdot \sin x+n\cdot \cos x\right)^2}dx}$\\\\\\ Now $\bf{x\cdot \sin x+n\cdot \cos x = \sqrt{x^2+n^2}\left\{\frac{x}{\sqrt{x^2+n^2}}\cdot \sin x+\frac{n}{\sqrt{x^2+n^2}}\cdot \cos x\right\}}$\\\\\\ Now Let $\bf{\frac{n}{\sqrt{x^2+n^2}}=\cos \phi}$ and $\bf{\frac{x}{\sqrt{x^2+n^2}}=\sin \phi}$\\\\\\ So $\bf{\tan \phi = \frac{x}{n}\Rightarrow \tan \phi = \tan^{-1}\left(\frac{x}{n}\right)}$\\\\\\ So $\bf{x\cdot \sin x+n\cdot \cos x = \sqrt{x^2+n^2}\cdot \cos \left(x-\phi\right)}$\\\\\\ So Integral is Convert into $\bf{\int\frac{1}{\cos^2\left(x-\phi\right)}\cdot \left(\frac{x^2+n(n-1)}{x^2+n^2}\right)dx}$\\\\\\ So Integral is $\bf{\int \sec^2 \left(x-\phi\right)\cdot \left(\frac{x^2+n(n-1)}{x^2+n^2}\right)dx}$\\\\\\ Let $\bf{(x-\phi) = t\Rightarrow \left(x-\tan^{-1}\left(\frac{x}{n}\right)\right)=t\;,}$ Then $\bf{\left(1-\frac{n^2}{x^2+n^2}\cdot \frac{1}{n}\right)dx = dt}$\\\\\\

\hspace{-20}$ So $\bf{\left(\frac{x^2+n(n-1)}{x^2+n^2}\right)dx = dt}$\\\\\\ So Integration is convert into $\bf{\int \sec^2\left(t\right)dt = \tan (t)+\mathbb{C}}$\\\\\\ $\bf{\Rightarrow \tan \left(x-\phi\right)+\mathbb{C}=\tan (x-\tan^{-1}\left(\frac{x}{n}\right))+\mathbb{C}}$\\\\\\ $\bf{\Rightarrow \frac{\tan x-\frac{x}{n}}{1+\tan x\cdot \frac{x}{n}}+\mathbb{C}=\left(\frac{n\cdot \tan x-x}{n+x\cdot \tan x}\right)+\mathbb{C}}$\\\\\\ So $\bf{\int\frac{x^2+n(n-1)}{\left(x\cdot \sin x+n\cdot \cos x\right)^2}=\left(\frac{n\cdot \tan x-x}{n+x\cdot \tan x}\right)+\mathbb{C}}$