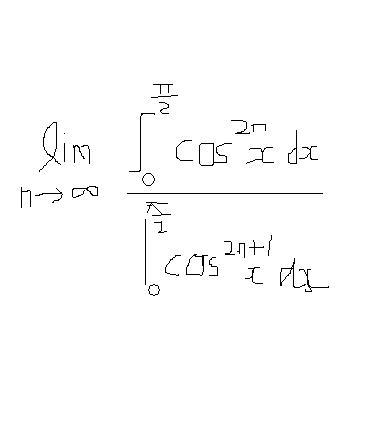a good exercise

can u plz post the solution.................

If 2n+1=a+1 and 2n=a, then the integral boils down to
{(a-1)(a-3)(a-5)....3.1.Î a(a-2)(a-4)...4.2}²
The limit of which as a→∞ turns out to be Π2......

your answer is wrong dude!!!

the options are 1/2,0,1,2

?????????

Consider the integral
I_n =\int_0^{\pi/2}\cos^nx\ \mathrm dx
We have
I_n =\int_0^{\pi/2}\cos^{n-1}x\cos x\ \mathrm dx =\left|\cos^{n-1}x\sin x\right|_0^{\pi/2} +(n-1)\int_0^{\pi/2}\cos^{n-2}x\,\sin^2x\ \mathrm dx
But sin² x = 1 - cos² x. Hence, we get
I_n =(n-1)\int_0^{\pi/2}\cos^{n-2}x\ \mathrm dx-(n-1)\int_0^{\pi/2}\cos^nx\ \mathrm dx
That is, we get
I_n = (n-1)I_{n-2}-(n-1)I_n
So that
\boxed{I_n = \dfrac{(n-1)}{n}\ I_{n-2}} -------(1)
Next, in the interval (0,\,\pi/2), the following inequality holds true:
\cos^{2n-1}x>\cos^{2n}x>\cos^{2n+1}x
Integrating from 0 to \pi/2, we get
I_{2n-1}\geq I_{2n}\geq I_{2n+1}
That is
\dfrac{I_{2n-1}}{I_{2n+1}}\geq \dfrac{I_{2n}}{I_{2n+1}}\geq 1 -------------- (2)
However, from (1), we get
I_{2n+1}=\dfrac{2n}{2n+1}\ I_{2n-1}
So that
\dfrac{I_{2n-1}}{I_{2n+1}}=\dfrac{2n+1}{2n}=1+\dfrac{1}{2n}
Hence, as n → ∞,
\dfrac{I_{2n-1}}{I_{2n+1}}\to 1
Therefore, from (2), by using the Sandwich principle, we get
\lim_{n\to \infty}\dfrac{I_{2n}}{I_{2n+1}}=1