1
1. \lim_{n \to \infty} (1 + sin\frac{a}{n})^{n}
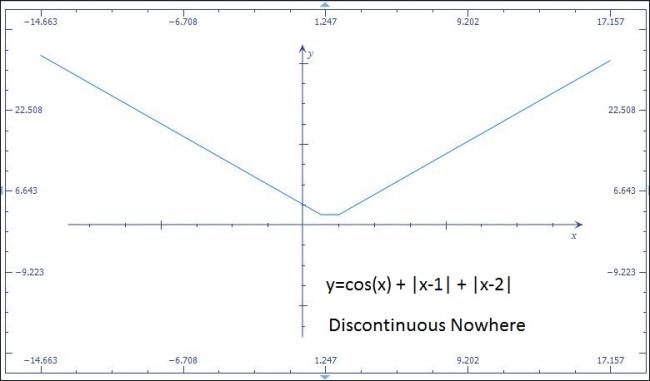
2. Function f(x) = (|x - 1| + |x - 2| + cosx), x\epsilon [0,4]
is discontinuous at how many points?
3. \lim_{n \to \infty} (\frac{1}{1.3} + \frac{1}{3.5} + \frac{1}{5.7} +....+ \frac{1}{(2n-1).(2n+1)})
-
UP 0 DOWN 0 0 13
13 Answers
11.ea ?
3.\frac{1}{(2n-1)(2n+1)}=\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})
hence :
\lim_{n\rightarrow \infty}\sum{\frac{1}{(2n-1)(2n+1)}}=\lim_{n\rightarrow \infty}\frac{n}{2n+1}=\lim_{n\rightarrow \infty}\frac{1}{2+\frac{1}{n}}=\frac{1}{2}
12.discontinuous no where....
3. use it as limit of sum yar.!!!! convert to definite integral...
1for 3. take Tn=.5[(2n+1)-(2n-1)]/(2n+1)(2n-1)
I think it will be 1/2
1for 3. take Tn=.5[(2n+1)-(2n-1)]/(2n+1)(2n-1)
I think it will be 1/2
1RPF!! if u add threee continuous functions...can u get a non-continuos function.....at the poins u said it will be non-differentiable!!
1
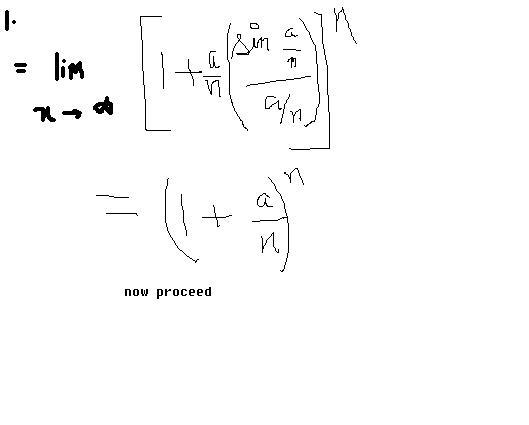
Lim n →∞ (1 + sin(a/n)n
= Lim n →∞ en{(1 + sin(a/n)-1}
= Lim n →∞ en sin(a/n)
= Lim n →∞ ea { sin(a/n)/ (a/n) }
= ea Lim n →∞ { sin(a/n)/ (a/n) }
=ea
62Q2..
THere are no discontinuities.. bcos the function is the sum of 3 continuous functions.. [1]
