Hint: The numbers a,b,c can be thought of as the roots of a cubic.
Let a<b<c be reals such that
a+b+c=6 and
ab+bc+ca=9
Then prove that
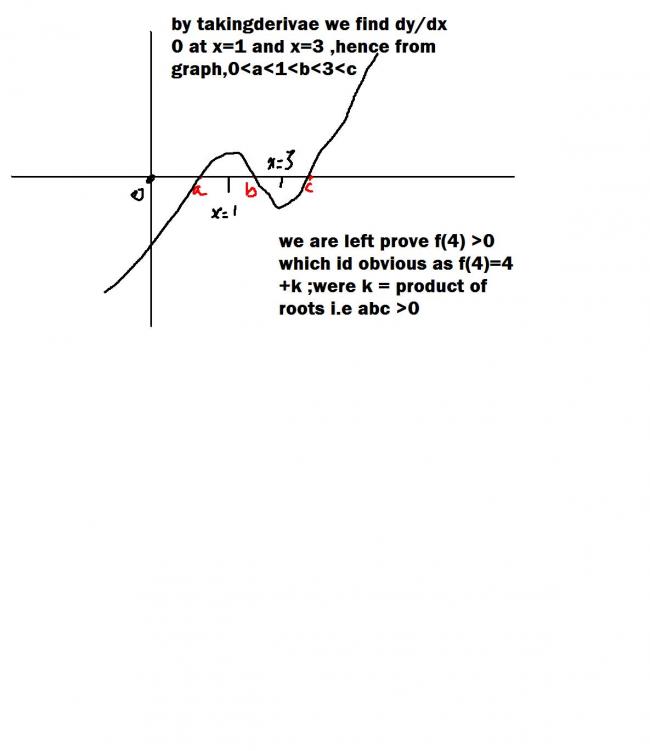
0<a<1<b<3<c<4
-
UP 0 DOWN 0 0 9

9 Answers
f(x)= x^3 - 6x^2+9x +k.
i think we hv to find out the derivative& equate to 0.
this gives the tangents at those pts to be parallel to x axis.
now we pull the graph by k upwards & down wards.
thus we get the required proof ensuring that the graph will not exceed 0&4.
this is just a hint.....
arpan .. very bad.. i did this one in the class and u are not letting others to do this :(
no you are correct..
but i din get why abc>0??
uptil the 1st derivative part and the graph you are correct..
but i guess i should not interfere too much in Kaymant sir's post...
srry!!!!!!!!!!
Nishant bhaiyya!!!!!!!
maafi chahta hoon!!!!!!!!!!!!!!!!