Anyone solve the first ques also!!!!!!!!!!!!!!!!!!!!!!
1)Is there any short cut method to solve this prob:
If f(x)=x+1/x, find f[f{f(x)}]
2)Can anyone show me the graph of cos√x?
-
UP 0 DOWN 0 0 10

10 Answers
2)the graph of cos√x is
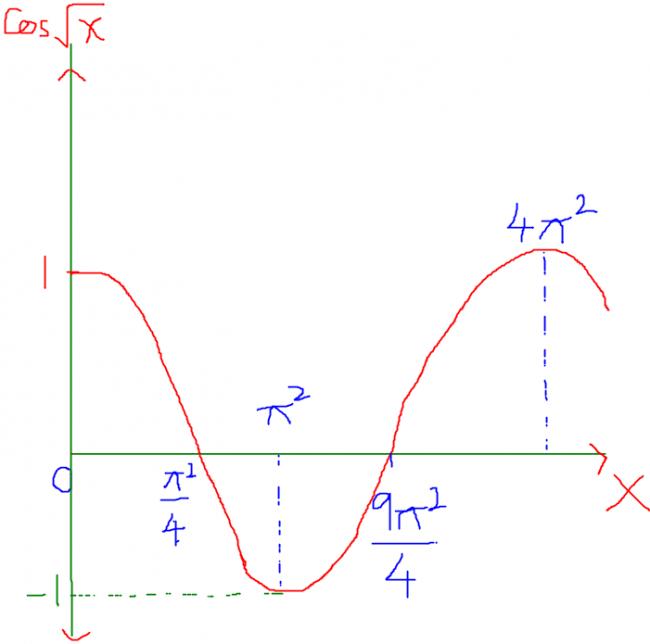
I hope that is clear!!
The graph doesnt exist for the negative values of x.
[339]
well how da hell did ya arrive at da ans..I dn't thick the ans is right either
(1)
assumin {.} = frac part [.]= great int
{f(x)} is some no <1 na ....
now f({f(x)}) is again <1 ....
so [.] of that is 0!!!!!!!
and f(0) = ∞
mr iitiamcoming
suppose
f(x)=0.5
then
{f(x)}=0.5
now
f(0.5)=0.5+2=2.5
which is not less than 1
so [f({f(x)})] cannot be zero
so the answer should be in terms of x and not any numerical value.....i hope u get the point
Can anyone finally solve the ques.
The answer is (x2+1)4+3x2(x2+1)2+x4 (x2+1)(x5+3x3+x)
Note '[.]'→ does not represent the greatest integer function.it is simply a bracket
Arpan, this is not very difficult..
You have to do the dirty work after this...
Think nicely...
Keep x+1/x= x2+1x
Then dont expand x2+1
And do this two times.... :)
Well i did this method only.And it is anything BUT short.So i was askin whether there was any other method or property by which I can solve this in 2-3 steps without doin the "dirty work."
No there is no nice method that I can think of... I Will be surprised if there is any!