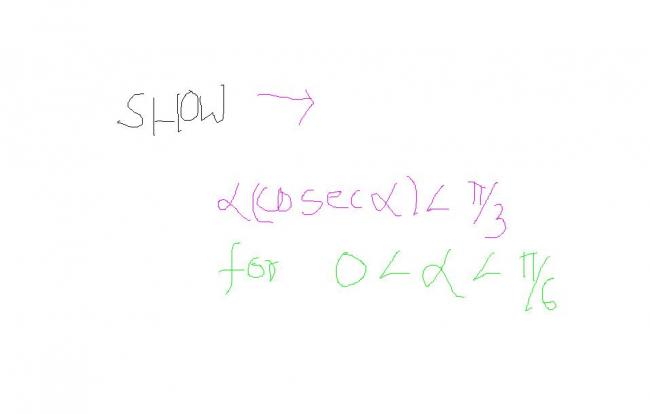application of derivatives

Consider f(x) = x - π3sinx

f(0) = f(Ï€6) = 0

f '(x) = 1 - π3cosx

f '(x) = 0 only at one point between 0 and π6 given by cosx = 3π

so between 0 and π6 the curve is either above x-axis or below x-axis

f ''(x) = π3sinx > 0, so the curve is concave upwards which means it lies below x-axis

so, f(x) < 0

x - π3sinx < 0

x(cosecx) < π3