Consider f(x)= ax2+bx+c, for |x|≤1.
a,b,c are real numbers.
If |f(x)| ≤1,
find the maximum value of |2ax+b|.
1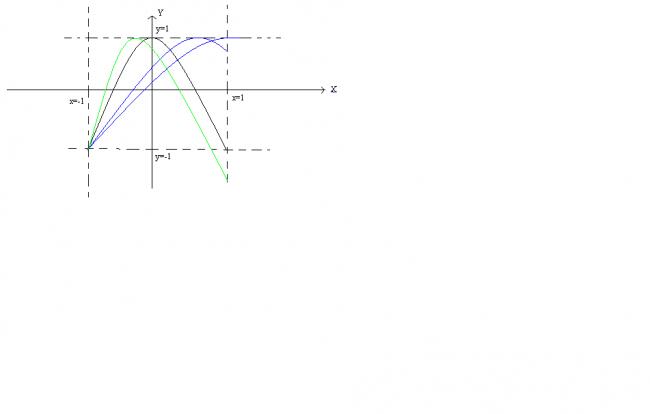
b555's method is really nice. Although I had actually solved in a different way (Gordo's proposal.)
As can be seen from the illustration----- the parabola that will contain the maximum slope will have the vertex at (0,1) and will pass through
(1,-1) and (-1,-1) OR will have a vertex at (0,-1) and will pass through
(-1,1) and (1,1)
Let us take the first one ( one could also take the 2nd one)
Equation:-
x2 = -4a(y-1)
It passes through (1,-1) and (-1,-1)
Putting the values, we get 4a = 1/2.
So, x2 = -(1/2)(y-1)
|dy/dx|=4|x|
|x|≤1
So, maximum of |dy/dx| = |2ax+b|= 4.
1yep got the concept..thanks guys..actually posted an incomplete soln earlier..here's how i did it:
let f(x)=y=ax2+bx+c
=>ax2+bx+c-y=0
now
x=[-b±√b2-4a(c-y)]/2a
=> 2ax+b=±√b2-4a(c-y)
=> |2ax+b| = √b2-4a(c-y)
from f(1)=f(-1)=1 and f(0)=-1
a=2, b=0, c=-1
hence substituting these values, we get the answer as 4
1yeah, i mean, by basic picture of a quadratic polynomial, we can say that /f'(x)/ is greatest at the end pionts of the domain in which u observe the function...now we can imagine that the derivative of the function at 1 or -1 can be high if, the graph is more dipped, and it is more evenly spaced ( i mean the dip point is not more to the left nor more to the right..) so to strike a combination of both these, we can get it when the dip point is at the origion ie the mid pt of 1 and -1..., and f(1)=f(-1), dis is further favoured if f(1) , f(-1) and the dip ie f(0) are as large as possible in magnitude, (in this case happens to be 1), so we get this way that our eqn. can be 2x2-1....thus f'(x)max=f'(1)=4...what b555 has done is mathamatical, what i have done is purely graphical...
cheers!!
39i cant do anything dude. just solved it way i could.
lets wait for metal`s solution
1Utna bhi difficult nahin hai-------- try to karo.
1 - 2 lines mein ho jayega , iff you think correctly :-)
1@metal... is it any no.?? or in terms of a,b,c ... i am getting in terms of a,b,c.
1I dont think so. In fact the maximum value will eb far lesser than 24.
You guys are thinking on complicated lines, it seems.
39good one metal. on solving we get
|a|≤8 |b|≤8 and even |c|≤1
|2ax+b|≤ |2ax| +|b|
|2ax| at most can be 16 and |b| can be atmost 8
so |2ax+b| has a maximum value of 24
