1
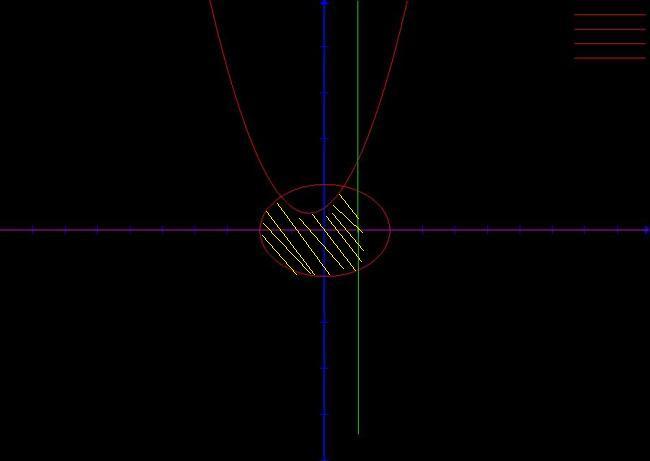
area of d shaded portion sld be found rit????????????is dat rit???????
Find the area bounded by the curves x2+y2=4, y=x2+x+1,
y=[sin2(x/4)+cos(x/4)] and the x-axis,where [.] denotes greatest integer function!!
-
UP 0 DOWN 0 0 44
44 Answers
1Sorry guys,
Instead of plotting y=1 graph,i plotted x=1 ,I'm sorry for the inconvenience!!!!!!! :( :( :(
1
1but ram the curve for 3rd dat is green one is wrong i guess
i tried to prove dat in my above posts
1seems 2 b a strght line.............not a curve.........v r sittin wit d same prob fr a lon time......
1leave it yaar........ i am blabberin smthn in sleep.....
1byah.... i need a 3d designer tool to design dis graph.....
62vishal... u need to realise that when we plot on the x and y axis.. we take length in radians .. not degrees :)
1ya true btw -2 to 2 acc to me cant say bout rest
will rechk tmorw
9the q is simple if u conc on
y = [ sin2 X/4 + cosX/4 ] within -2,2
it is always greater than 1 as y = [ 1 - λ2 + λ] λ ≥λ2 as its cosθ
so dia reduces to parabola ,circle, y = 1 and 0
just find intersection and integrate areas
11Won't any GIF have a graph with horizontal stripes? ONly where the stripes come and at what intervals they come is decided by the nonsense inside. Anyway x can be in radians as well! You ppl took x as 120 deg. For all we know, it can be 2Ï€/3 !
341The expression y = sin2(x/4)+ cos (x/4)
= 1-cos2(x/4) + cos (x/4)
= 1 + cos (x/4) [1-cos (x/4)]
Here we must remember that -1/2≤x/4≤1/2
So cos (x/4) will always be positive
So recalling that when 0≤t≤1, t(1-t) lies between 0 and 1/4,
the given expression lies between 1 and 5/4 (Of course t will be greater than 1/2, so 5/4 is not attained)
In any case [ 1-cos2(x/4) + cos (x/4)] = 1 for this range
So this function is just y = 1
edit: typo indicated by aragorn corrected
1thanks prophet i was shouting yesterday dat its =1
bt never thougt like this
thanks again:)
1sry correctn for u bro
dat is fr x=720 & radious of cicle = 2 so no need to wry bout dat
1BUT SKY... can u plz tell me where dat parabola cuts d axis?????
62y=x2+x+1,
This is (x+1/2)2+3/4
So this will be a parablola on x=-1/2 and 3/4 units above the x axis!! :)
y=[sin2(x/4)+cos(x/4)]
find when will sin2(x/4)+cos(x/4)=1 and sin2(x/4)+cos(x/4)=0
and also when it will be -ve!
This is the rough outline of plotting the graph
To be fair it is a tough question.
11Well, Nishant. that's the problem. the graph of y=[sin2(x/4)+cos(x/4)] is so tough to plot.
62yeah it is aragon
that is why i said that u need to find the points where the value of this expression is 0, 1, -1 etc
then in between we will have to unse greatest integer function :)
1is 3rd one a const func i am gettin it 1 for many Q
Q=angles