 62
62it is very much in the syllabus..
Se here what our approximation is that the slices are cyllindrical..
and your doubt is very genuine..
when we are finding volume we take the volume as height times surface area
When we take area we take perimeter times Width
Now when we are taking area, the perimeter is 2 pi r
the width is dl or dh? (what do you think :)
 1
1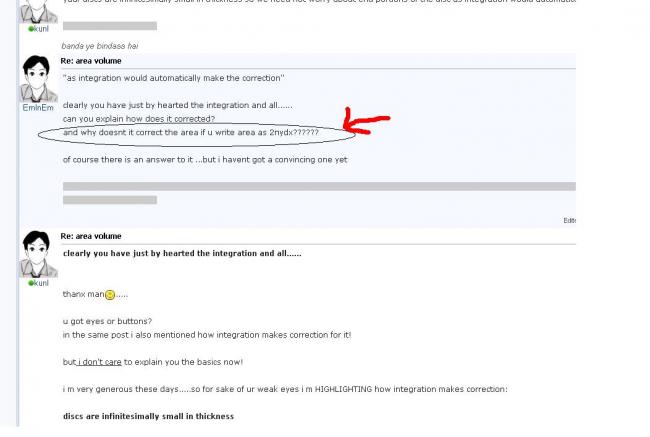
srry if i m not generous ...
btw u actually havent yet understood what my doubt is
i want to use your same arguement "discs are infinitesimally small in thickness" and hence write area ∫2πydx
even buttons work for me !!
 1
1clearly you have just by hearted the integration and all......
thanx man[1].....
u got eyes or buttons?
in the same post i also mentioned how integration makes correction for it!
but i don't care to explain you the basics now!
i m very generous these days.....so for sake of ur weak eyes i m HIGHLIGHTING how integration makes correction:
discs are infinitesimally small in thickness
 1
1"as integration would automatically make the correction"
clearly you have just by hearted the integration and all......
can you explain how does it corrected?
and why doesnt it correct the area if u write area as 2Ï€ydx??????
of course there is an answer to it ...but i havent got a convincing one yet
i dont have common sense like you and i cant keep anything in mind that isnt convincing ...may be you got the ability of by hearting even wat you dont understand completely
 1
1yaar discs are infinitesimally small in thickness so we need not worry about end portions of the disc as integration would automatically make the correction.
bhai use common sense
 1
1@ kunl u didnt understand my doubt ...
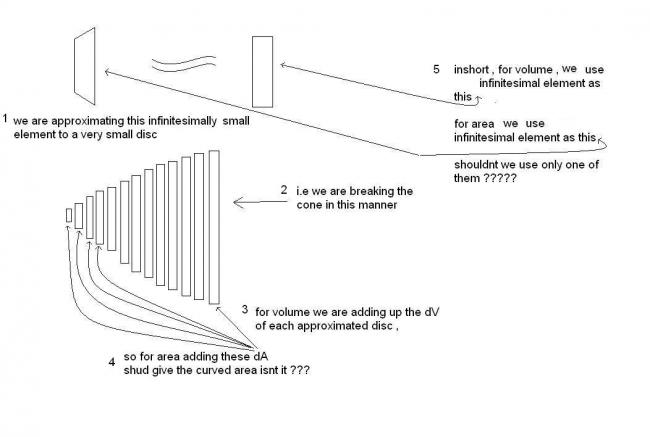
can u plz explain why is your volume ∫πr2dLcosθ and not ∫(πr2dx+ πydydx) ,
where πydydx is the volume u missed to write ...
can u please explain how is the approximation in volume accounted ...
if u can explain that , then why isnt approximation in area accounted iff we write area as ∫2πydx
where x is height and y is radius at x and L is slant height
INTEGRATING THE INFINTESIMAL VOLUME/AREA ISNT MY DOUBT ...FINDING THE INFINITESIMAL VOLUME /AREA ITSELF IS MY DOUBT !!
 1
1mine version:[completely within JEE SYLLABUS [1]]
take variable x along slant of cone and @ be semi vertical angle,r be radius of small horizontal discs sliced from cone!
L=slant height,R=radius of cone and H=height

 1
1i m curious to know what solution is in the mind of prophet sir !!!
 1
1at last ... someone did help !! thanx nishant bhaiyya and pritish !!!
i got the points in #13 & #14 ,
nishant sir i agree that area shud always be ∫2πydL
an easier proof goes like this
dA can be treated as an area vector and it has 2 components, 2Ï€ydx & 2Ï€ydy
hence |dA |= ( (2Ï€ydx)2+ (2Ï€ydy)2 )1/2 = 2Ï€ydx (1+(dy/dx)2)1/2
and this is exact and without any approximation ,
but in calculating volume we make an approximation ,
we say that the volume of disc will be πy2dx ,
but that isnt even a perfect disc, and we are neglecting some volume , i.e 12 x (2πydy) x (dx) = πydydx
why does approximation work in volume calc but not in area ...
( in area if we use ∫2πydx the error adds up to πR(L - H) !!! )
 62
62wow.. pritish.. this is a bit too much for an average aspirant ;)
Most of the time they will not need it even though many coaching institutes do tell this and I belive what pritish has written should be understood by every aspirant who is aiming for the top concepts [1]
But the minimal understanding needed is what I said in the post before.. ;)
 39
39Well..if Nishant sir says it's genuine, my apologies :) I never did this concept before my first sem of engineering, hence the misunderstanding.
You do know where ∫2πy (1 + (dy/dx)2)1/2 dx came from right?
If not, let me explain...this may be unnecessary, but it may help you in understanding the basic concept behind this. Suppose we have a curve AB defined by y = f(x), assuming it doesn't cut the X-axis. We take two points P(x, y) and Q(x + dx, y + dy) on it. Now the difference in the methods of calculating volume and area is this :
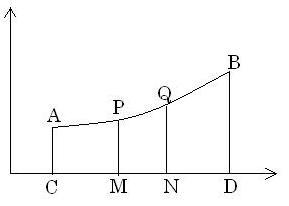
For area, we take the length of the arc PQ as ds and that of AP as s(making AQ = s + ds). If we drop perpendiculars C from A, M from P, N from Q and D from B, then 'S' denotes the curved surface area generated by revolving the area CMPA about the X-axis. dS is the curved surface generated by revolving MNQP. We assume that the curved area generated by revolving MNQP lies between curved surfaces of right circular cylinders whose radii are PM and NQ, which are of the same thickness ds.
which => 2Ï€yds < dS < 2Ï€(y + dy)ds (obviously!!)
=> 2Ï€y < dSds < 2Ï€(y + dy)
As Q→P or as ds→0, dy→0.
Thus we get dSds = 2Ï€y
=> dS = 2Ï€yds
We integrate within curve limits to get S, which is what we need.
∫2Ï€yds = ∫2Ï€ydsdxdx which gives your relation as dsdx = √1 + (dydx)².
Now you can apply this to the specific case of a cone, which is obtained by revolving a right angle triangle about it's perpendicular.
We use a different procedure for volume calculation where we get dVdx = πy² and πy² < dV/dx < π(y + dy)².
It's much simpler to think the way Nishant sir has, though :P
 1
1is the concept too tough ?????????????
 1
1subhodip i know that derivation very well ....u didnt get what my doubt is please read wat i hav written in post 1
 21
21i use to calculate the volume of cone that way
http://www.targetiit.com/iit-jee-forum/posts/can-someone-help-18336.html
the curved area can also be calculated similarly
 39
39Volume and surface integrals are taught in the first year of engineering....this isn't in the syllabus of JEE and neither is this basic JEE level. Nice doubt though, but I'm not the right person to answer it. All I ask is that you stop spamming other threads with this link in the hope that Nishant sir will take notice, it is really irritating. All you'll get is your threads and posts deleted if you keep doing that.
Why don't you add him on gmail and ask personally?
 1
1come on guys this is basic if u cant solve this how do u expect to crack jee pls help me
 1
1prophet sir + nishant sir + kaymant sir helpp




