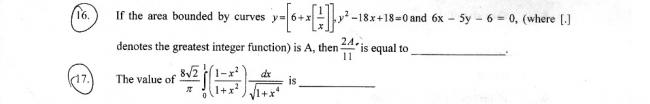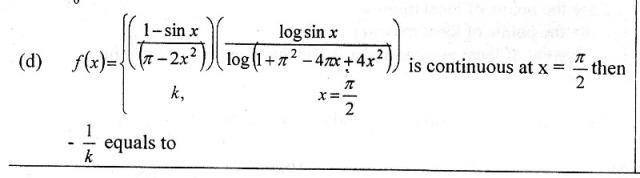Calculus

\hspace{-16}(17)\;\; \int_{0}^{1}\frac{(1-x^2)}{(1+x^2).\sqrt{1+x^4}}dx$\\\\\\ $=\int_{0}^{1}\frac{(1-x^2)}{x.(x+\frac{1}{x}).x.\sqrt{x^2+\frac{1}{x^2}}}dx$\\\\\\ $=-\int_{0}^{1}\frac{(1-\frac{1}{x^2})}{\left(x+\frac{1}{x}\right).\sqrt{(x+\frac{1}{x})-\left(\sqrt{2}\right)^2}}dx$\\\\\\ Now Put $\left(x+\frac{1}{x}\right)=t\Leftrightarrow \left(1-\frac{1}{x^2}\right)dx=dt$\\\\ and Changing The Limit, we get\\\\ $=\int_{2}^{\infty}\frac{1}{t.\sqrt{t^2-\left(\sqrt{2}\right)^2}}dt$\\\\ now Put $t=\sqrt{2}.\sec \theta\Leftrightarrow dx=\sqrt{2}.\tan \theta.\sec \theta.d\theta$\\\\ and Changing Limit.\\\\ $=\int_{\frac{\pi}{4}}^{\frac{\pi}{2}}\frac{\sqrt{2}.\sec \theta.\tan \theta.d\theta}{\sqrt{2}.\sec \theta.\sqrt{2}.\tan \theta}$\\\\\\ $=\frac{1}{\sqrt{2}}.\int1.d\theta =\frac{1}{\sqrt{2}}.\theta\Bigint|_{\frac{\pi}{4}^{\frac{\pi}{2}}}$\\\\\\ $=\frac{1}{\sqrt{2}}.\frac{\pi}{2}$\\\\

\hspace{-16}$So Value of $\frac{8.\sqrt{2}}{\pi}.\int_{0}^{1}\frac{(1-x^2)}{(1+x^2).\sqrt{1+x^4}}dx$\\\\\\ $=\frac{8.\sqrt{2}}{\pi}.\frac{\pi}{2.\sqrt{2}}=4$

\hspace{-16}$I Think the last Question like in this way::\\\\ (d)::\;\;If $f(x)=\left\{\begin{matrix} \displaystyle \frac{1-\sin x}{\left(\pi-2x\right)^2}.\frac{\ln \sin x}{\ln \left(1+\pi^2-4\pi.x+4x^2\right)} \;\;,& \displaystyle x\neq \frac{\pi}{2}\\\\ k\;\;,& \displaystyle x=\frac{\pi}{2} \end{matrix}\right.$\\\\\\ If $f(x)$ is Conti. at $x=\displaystyle \frac{\pi}{2}$. Then $-\frac{1}{k}=$