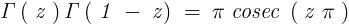Definite

Obviously , the antiderivative of the given function ( which , in this case , turns out to be a

Hypergeometric series ) is not so easy to find . Also the integration must be carried out in a

manner in which convergence issues must be taken care of . But since here " n " is given to

be a natural number , so we need not worry about them . However a stricter condition

would have been ;

Real Part Of " n " > 1 .

I denote the original integral as " I " .

Now in the original integral , let us substitute

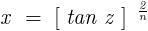
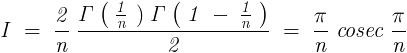
Here , I used two standard identities involving Gamma functions . The first one is -

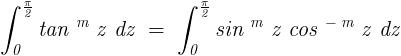
which is nothing but ,

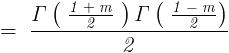
And the second one , commonly referred to as Euler ' s Reflection Formula is -

Another thing that struck me while I pondered over the solution is that the usage of complex

integration , i . e , Contour Integration may have been an efficient way , but still , I think that would

require a high skill in Complex Analysis which I obviously lack .