how ,please post solution
12 Answers
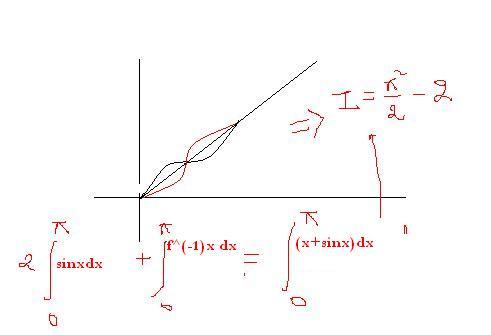
sorry if bit too unclear
RED line is f-1(x) . Black line is f(x)
thank you friends for the solution, but i did it in another way. tell me if my solution is correct
i derived f-1(x)=x-sinx and then integrated it over 0 to pi.
no it doesnt there are a few subtle differences..
This was discussed sometime back and answered quite nicely by kaymant sir... Let me search for it
We can't find f-1(x) that way.
We know that fof-1(x) = x
That means sin(f-1(x)) + f-1(x) = x
I don't think you can isolate f-1(x) from here.
It is easy to see that f^{-1} (0) = 0; f^{-1} {\pi} = \pi
We have to find \int_0^{\pi} f^{-1} (x) \ dx
Let x = f(y).
Then the integral is \int_0^{\pi} y (1+\cos y) \ dy.
By partial integration you get \frac{\pi^2}{2} - 2
There's some theorem with integrals of f(x) and f-1(x) which was discussed in this forum long back which I suspect simplifies these problems. I'll try to locate that thread

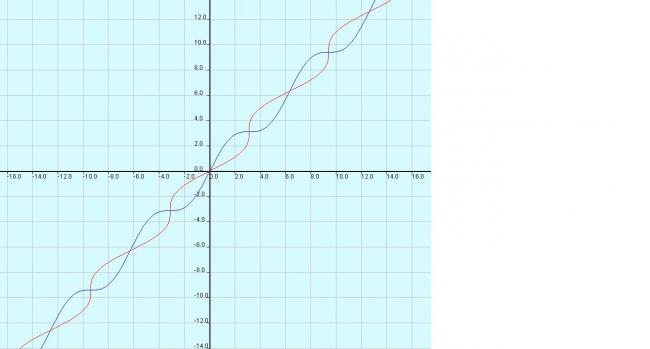
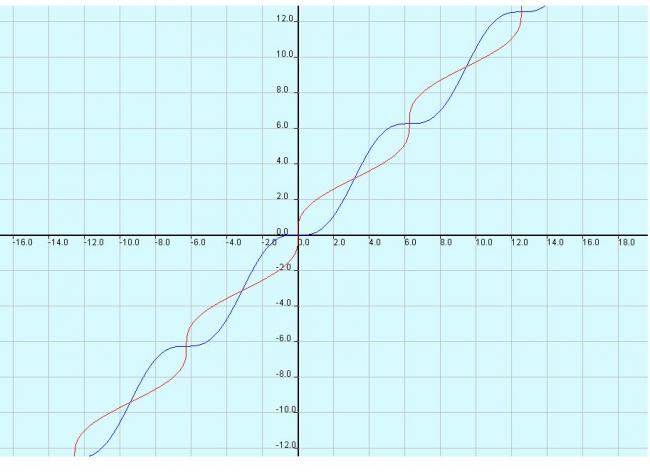 and its inverse(red)
and its inverse(red)