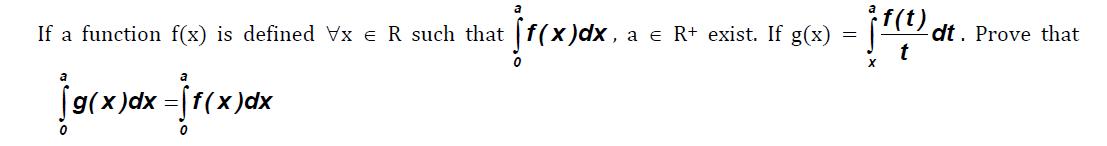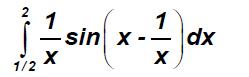Definite integration

\hspace{-16}\bf{\int_{\frac{1}{2}}^{2}\frac{1}{x}.\sin \left(x-\frac{1}{x}\right)dx}$\\\\\\ Put $\bf{x-\frac{1}{x}=t\Leftrightarrow \left(1+\frac{1}{x^2}\right)dx=dt}$\\\\\\ $\bf{dx=\frac{x^2}{(1+x^2)}dt}$ \\\\\\ and Changing Limit, We Get \\\\\\ $\bf{\int_{-\frac{3}{2}}^{\frac{3}{2}}\sin (t).\frac{x}{(1+x^2)}dt=\int_{-\frac{3}{2}}^{\frac{3}{2}}\sin (t).\frac{1}{\left(x+\frac{1}{x}\right)}dt}$\\\\\\ and above Given $\bf{\left(x+\frac{1}{x}\right)^2=\left(x-\frac{1}{x}\right)^2+4}$\\\\\\ $\bf{\left(x+\frac{1}{x}\right)=\sqrt{\left(x-\frac{1}{x}\right)^2+4}=\sqrt{t^2+4}}$\\\\\\ So $\bf{I=\int_{-\frac{3}{2}}^{\frac{3}{2}}\sin (t).\frac{1}{\sqrt{t^2+4}}dt=0}$\\\\\\ bcz $\bf{f(t)=\frac{\sin(t)}{\sqrt{t^2+4}}=}$Odd function \\\\\\Using $\bf{\int_{-a}^{a}f(x)dx = 0}$\\\\\\ If $\bf{f(x)=}$ Odd function..........

\hspace{-16}\bf{(2)\;\; g(x)=\int_{x}^{a}\frac{f(t)}{t}dt................(1)}$\\\\\\ Now Diff. both side w.r.to $\bf{x}\;,$ We Get\\\\\\ $\bf{g\hspace{-10}\quad'(x)=-\frac{f(x)}{x}..............................(2)}$\\\\\\ Put $\bf{x=a}$ in equ.....$\bf{(1)}\;,$ We Get\\\\\\ $\bf{g(a)=0}$\\\\\\ Now from equation $\bf{(2)}\;,$ We Get\\\\\\ $\bf{x.g\hspace{-10}\quad'(x)=-f(x)}$\\\\\\ Now Integrate both side with Limit...... $\bf{0}$ to $\bf{a}$\\\\\\ $\bf{\int_{0}^{a}x.g\hspace{-10}\quad'(x)dx=-\int_{0}^{a}f(x)dx}$\\\\\\ $\bf{\left. \left(x g(x)\right)\right|_0^a -\int_{0}^{a}g(x)dx = -\int_{0}^{a}f(x)dx}$\\\\\\ So $\bf{a.g(a)-0.g(0)-\int_{0}^{a}g(x)dx=-\int_{0}^{a}f(x)dx}$\\\\\\ So $\bf{\int_{0}^{a}g(x)dx=\int_{0}^{a}f(x)dx}$