The tangent at a point P(x, y) on a curve meets the axes at P1 and P2 such that P divides P1P2 internally in the ratio 2 : 1. The equation of the curve is
1. xy = c
2. x2y = c
3. xy2 = c
4. none of these
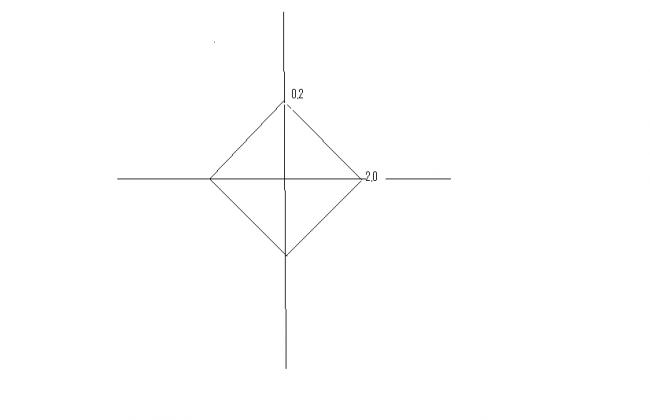
11A point 'P' moves in xy plane in such a way that [| x | + | y |] = 1, where [.] denotes the greatest integer function. Area of the region representing all possible positions of the point 'P' is equal to
1. 4 sq units
2. 16 sq units
3. 2√ 2 sq units
4. 8 sq units
21saket dude subtract the inner rombus!!!
u'll get da ans...
[|x|+|y|]=0
subtract this portion frm ur area
11actually vaise mera 2nd ques yeh tha
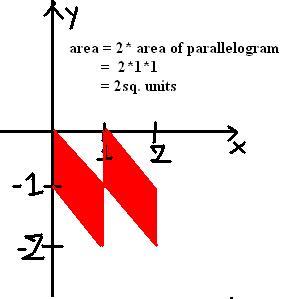
Q. 18 A point 'P' moves in xy plane in such a way that [x + y + 1] = [x], where [.] denotes the greatest integer function, and x (0, 2). Area of the region representing all possible positions of the point 'P' is equal to
a 2 sq units
b 8 sq units
c 2 sq units
d 4 sq units
106for this one:
[x+y+1] = [x]
==> [x+y] + 1 = [x]
When x ε (0,1), [x] = 0
So, [x+y] = -1
i.e. -1≤x+y<0
When x ε [1,2) then [x] = 1
then [x+y] = 0
==> 0≤x+y<1
i think now u can draw graph and easily find area.... im uploading graph in next post..
1method may be let the slope at P be y' of the tangent
then form the equation of a staight line
taking P1 on Yaxis
and P2 on Xaxis
from the eq putting x=0,
and y=0
we get P1 as (0,y-xy')
and P2 has y coord. as 0
so by 2:1 ratio and using Y coord....ek diff equation ae solve to get
x2y=c
