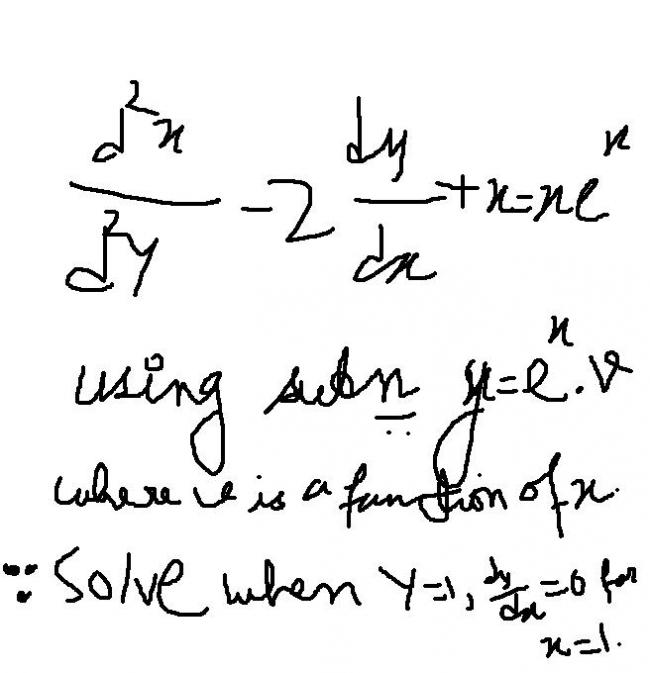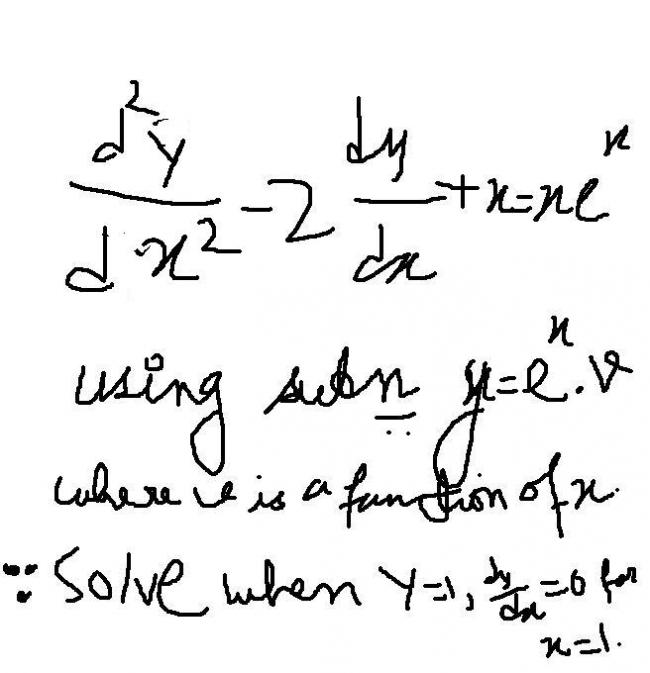yes eureka...evenmera bi ho gaya...will u see the oder differential equations i have posted???
7 Answers
\\y=e^x\times v \\\frac{dy}{dx}=e^x\times v+e^x\times \frac{dv}{dx} \\\frac{dx}{dy}=\frac{1}{e^x\times v+e^x\times \frac{dv}{dx}} \\\frac{d^2x}{dy^2}=\frac{-1}{(e^x\times v+e^x\times \frac{dv}{dx})^2}\times (e^x\times v+2e^x\times \frac{dv}{dx}+e^x\times \frac{d^2v}{dx^2}) \\\frac{d^2x}{dy^2}=\frac{(e^x\times v+2e^x\times \frac{dv}{dx}+e^x\times \frac{d^2v}{dx^2})}{(e^x\times v+e^x\times \frac{dv}{dx})^2}\\\frac{d^2x}{dy^2}=\frac{(v+2 \frac{dv}{dx}+ \frac{d^2v}{dx^2})}{e^x(v+\frac{dv}{dx})^2}
I dont see this taking us anywhere far.. may be i need to rework something..
are you sure it is d^2x/dy^2 and not d^2y/dx^2???
\\y=e^x\times v \\\frac{dy}{dx}=e^x\times v+e^x\times \frac{dv}{dx} \\\frac{d^2y}{dx^2}=(e^x\times v+2e^x\times \frac{dv}{dx}+e^x\times \frac{d^2v}{dx^2}) \\\frac{d^2y}{dx^2}-2\frac{dy}{dx}=(-e^x\times v+e^x\times \frac{d^2v}{dx^2})
I dont seem to be heading anywehre though!
\frac {d^2y}{dx^2}-2\frac {dy}{dx}+x=xe^x
Put \ y=e^x.v
=>\frac {dy}{dx}=e^xv+e^x\frac {dv}{dx}=>\frac {dy}{dx}=y+e^x\frac {dv}{dx}=>\frac {d^2y}{dx^2}=\frac {dy}{dx}+e^x\frac {dv}{dx}+e^x\frac {d^2v}{dx^2}=>\frac {d^2y}{dx^2}=\frac {dy}{dx}+(\frac {dy}{dx}-x)+e^x\frac {d^2v}{dx^2}
=>\frac {d^2y}{dx^2}=2\frac {dy}{dx}-x+e^x\frac {d^2v}{dx^2}=>\frac {d^2y}{dx^2}-2\frac {dy}{dx}+ x=e^x\frac {d^2v}{dx^2}
=>e^x\frac {d^2v}{dx^2}=xe^x=>\frac {d^2v}{dx^2}=x
Now its solvable[1]