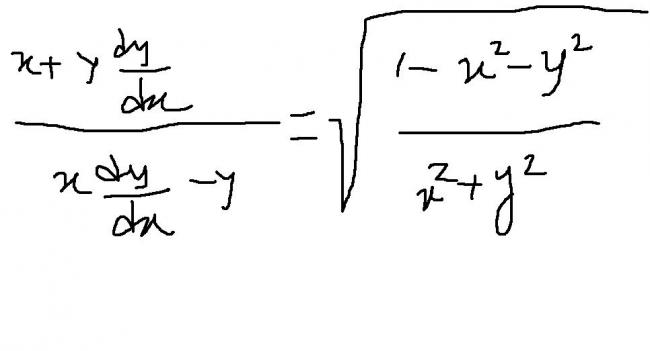differential equation challenge 8

polar coordinates are to help over here!
let x= rcosθ and y=r sinθ, so that x²+y² =r² (eqn 1)and tan θ=y/x (eq 2)
thus, from eq (1) d(x² +y²) = d(r²)
=> x dx +y dy =r dr (eq 3)

from eq 2 d(y/x)= d(tan θ)
=>(x dy -y dx)/x² =sec²Î¸ dθ
=> x dy - y dx = x²sec²Î¸ dθ = r² cos²Î¸ sec²Î¸ dθ(eq 4)

from 3 and 4 we have (r dr)/r² dθ =√{(1-r² /r²)} i.e. dr/√(1-r²) = dθ
=> sin^-1(r) =θ +c
=> r= sin θ +c =>√(x² +y²) = sin {c+ tan^-1(y/x)}

thus we have the results easily !