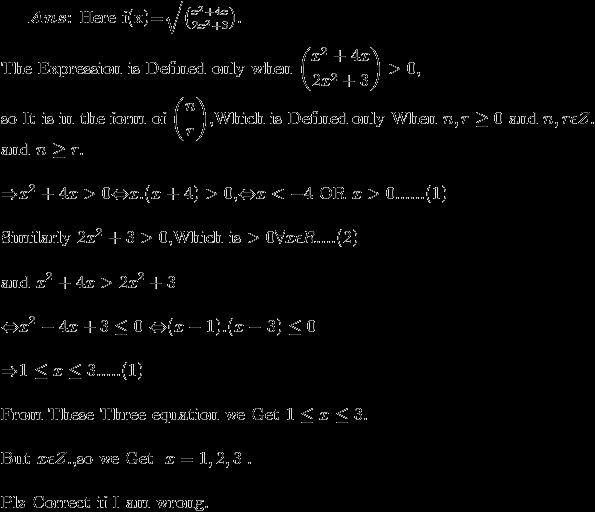Domain - Functions

1) f(x) = √x² - |x| - 2
We impose various restrictions(set theory ke mutaabik) as per definition of functions involved. Then we take intersection of those restrictions to get the domain.

R1 : Square root function. For √x, x ≥ 0.
So x² - |x| - 2 ≥ 0
=> |x|² - |x| - 2 ≥ 0 (As x² is the same as |x|²)
=> (|x| + 1)(|x| - 2) ≥ 0
Using the wavy curve method, we can easily see that |x| ≤ -1 U |x| ≥ 2 for the inequality to be satisfied(where U is union).
As |x| ≤ -1 is not possible, we discard it from the union(As any set U Null set = the set itself).
So |x| ≥ 2 or x ≤ -2 U x ≥ 2.
Hence R1 -> x ≤ -2 U x ≥ 2

R2 : Modulus function. For |x|, x ≥ 0.
Here simply x ≥ 0.

Now taking intersection, R1 ∩ R2 => x ≥ 2 is the domain of the function...

2) Dunno bout this one...it never came right for me when I tried it.

3) You have to be careful of the base of the logarithms here.
As per def of log function,
log₂log_2/Ï€(Y) ≥ 0 where Y is (tan^-1x)^-1 for simplicity.
=> log₂log_2/Ï€(Y) ≥ log₂1
=> log_2/π(Y) ≥ 1
=> log_2/π(Y) ≥ log_2/π(2/π)
=> Y ≤ 2/π [Note the inequality change, this is because logarithm base was smaller than 1].
=> 1/tan^-1x ≤ 2/π
I think we can cross multiply. This is because 1/tan^-1x will have to be positive anyway, for the rest of the logs to work. Sooo...
=> tan^-1x ≥ π/2...
Feeling sleepy...lol...I'll be back for the rest later [13]

1) case 1 .. x>0 then

f(x)=√x²-x-2

x²-x-2>= 0

(x-2) (x+1) >= 0

so, x E (-∞,-1] U [2,∞) but we have taken x>0 ,hence

x E [2.∞) ........1

case 2....x<0 then

f(x)=√x²+x-2

x²+x-2>= 0

(x+2).(x-1) >=0

x E (-∞,-2] U [1,∞) but we have taken x<0 .so

x E (-∞,-2] .........2

using 1 and 2

x E (-∞,-2] U [2,∞) .............3

or x E {R - (-2,2)}

OPEN BRACKETS BECAUSE -2 AND 2 ARE INCLUDED IN THE DOMAIN OF THE GIVEN FUNCTION AS U CAN SEE FROM EQ. 3

4) For this one, we'll have a bunch of tricky restrictions. x² + 4x and 2x² + 3 will have to be positive integers. I won't be going into non-integer factorials, because those require gamma functions/integrals...not sure whether those are in JEE syllabus.

R1 : Square root function.

^{x² + 4x}C_{2x² + 3} ≥ 0
=> Always true. x belongs to the integer set Z⁺.

R2 : Positivity of numbers being operated on by C.

x(x + 4) > 0
=> x < -4 U x > 0

AND

2x² + 3 > 0
=> x can be any value.

Taking intersection, finally R2 is x < -4 U x > 0.

R1 ∩ R2 gives the domain as integers less than -4 and greater than 0. If there is a better way to solve this, I'd love to know..

5) For the GINT function, here's an exhaustive collection of properties -: http://www.targetiit.com/iit-jee-forum/posts/greatest-integer-function-exhaustive-collection-pl-13636.html. Check out the last(mine) post too.

f(x) = sin^-1[2x² - 3]

R1 : Arcsin input always lies between -pi/2 to pi/2.

-pi/2 ≤ [2x² - 3] ≤ pi/2
We check these out separately.

[2x² - 3] ≥ -pi/2

The equal to part is not possible as the LHS is an integer and the RHS is not.
So [2x² - 3] > -pi/2 or > -1.57
This can be written as [2x² - 3] ≥ -1 so that both sides are integral.
For the output of the GINT function to be an integer greater than or equal to -1, 2x² - 3 ≥ 0 OR 2x² - 3 = -1.

So x ≤ -√3/2 U x ≥ √3/2 U {1, -1}

Similarly do [2x² - 3] ≥ pi/2 and take the intersection of both cases to get the domain...phew.

3rd one
y= log_{10}log_{2}log_{2}log_{2/\pi}(\frac{1}{tan^{-1}x})

\Rightarrow log_{2}log_{2}log_{2/\pi}(\frac{1}{tan^{-1}x})>0

\Rightarrow log_{2}log_{2/\pi}(\frac{1}{tan^{-1}x})>1

\Rightarrow log_{2/\pi}(\frac{1}{tan^{-1}x})>2
\Rightarrow 0<(\frac{1}{tan^{-1}x})< (\frac{2}{\pi })^{2}

i.e \Rightarrow \infty>tan^{-1}x >(\frac{\pi}{2})^{2}

wich isnt possible ,
hence domain is an empty set ( if i didnt miss anything)

Thanks a lot Pritish for the detailed explanation.[1]

@Mavarick, thanks a lot. You din make any mistake while solving the questions [1], nice explanation and solution[1]
You did a small mistake in the 5th question while solving
[2x²-3] < 2

here x will lie between -√(5/2) and √(5/2), Qwerty has given the solution too.

Thanks a lot Nihal and Qwerty [1]

for 2nd one

case (i) | x | > 1

thus x⁸ + 1 + 1 > x⁸ + 1

thus x⁴(x⁸ + 1) + 1 > x (x⁸ + 1)

i.e x¹² + x⁴ + 1 > x⁹ + x

hence all x satisfying |x| > 1 are in domain

now case (ii)

|x| ≤ 1
i.e x is a fraction
hence x⁴ > x⁹

1 > x

x¹² > 0

hence

x¹² + x⁴ + 1 > x + x⁹

hence all x satisfying |x| ≤1 also lie in the domain

hence all reals lie in the domain