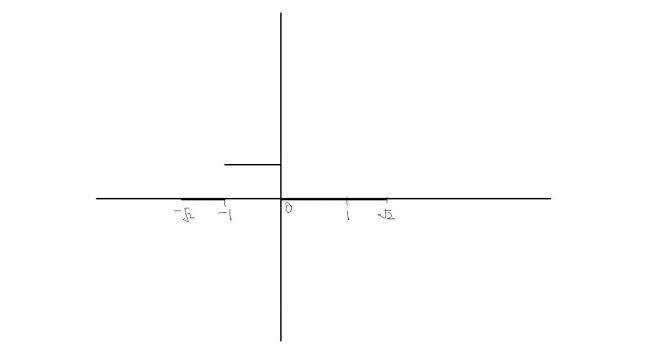
For this ques u have to remember that
[x]=0 when x→(0,1) ; [x]=1 when x→(1,2) ;[x]=-1 when x→(-1,0)
[x2]=0 when x→(0,1) ; [x2]=1 when x →(1,√2) ;[x2]=0 when x→(0,-1) ;[x2]=1 when x→(-1,-√2)
The funtion f(x) = [x]2 - [x2] (where [] is GIF) is discontinuous at
a.All integers
b.All integers exvept 0
c.All integers except 1
d.All integers except 0 and 1
-
UP 0 DOWN 0 0 11

11 Answers
Can u pls show that here mani...I find it difficult..
Todays's GON(graph of the night)
draw the graph for above funtion
@mani but ans given is it is continuous at 0!!
@msp adei...ans given was c..(why did u pink ur post if u r not sure it is correct??[3])
ans is c
for 1 its continuous ( f(1+) =f(1)= f(1-) =0 )
for 0 discontinuous ( f(0) =0 f(0+)=0 f(0-)= 1 )
mani is graph in #7
absolutely correct ??
pls chk for x = - 1.2
but i think we r concerned with -1,1
u r perfectly apt in ur statement !!!!!!!!!!!
but it doesen't affect the answer [1]