What is the condition that the equation ax2+bx+c has a root in [0, 1]?
In class, we integrated the given expression and arrived at the condition a3+b2+c=0. However, if we take the equation (x-2)(x-0.5)=0 ie x2-52x+1=0, we get a=1, b=-52, c=1 which does not satisfy the derived condition but obviously has a root between 0 and 1.
Where did we do wrong?
-
UP 0 DOWN 0 0 2
2 Answers
171
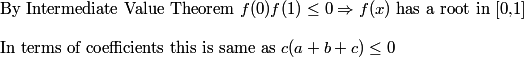
However be warned that this a sufficient and not a necessary condition as you could have f(0) f(1)>0 and have both roots in that interval.
Similarly when you integrate over that interval you could the value as positive, negative or zero.
If the integral is zero we know that the function changes sign in that interval and hence must attain its zero there. Thus it is sufficient but not necessary.
The implication is only one way and not both ways
Soumyadeep Basu Yes, I also thought that this was the problem. Do you know of a way to solve the question?Upvote·0· Reply ·2013-07-01 09:32:42
171The condition I mentioned becomes necessary and sufficient for exactlyone root in [0,1]