 1
1FOR -VE SLOPE GRAPHS U CAN USE FOLLOWING FORMULA------
-------------------------------------------------------------------------
∫f-1(x)dx=∫f(x)dx + af(a)-bf(b).
but i would suggest simply draw the graph(even roughly) to see what is required
to be done.
 62
62The explanaiton of this thing is that The integral gives the algebriac sum.. which means one area is -ve in magnitude :)
 1
1i m still on my answer...
 1
1thik hai dost kal discussiayenge isko...:)(agar mere dost ne mere ko lappy use karne di toh..:))
 33
33aj jaane do...
kal tak jo galat hai dono me uska dimag khul jaega...
kal discuss karenge isko..
[1]
 1
1hey abhishek u used the eqn:y=(x-2)2
tell me what was in lhs?
and rhs?
 33
33its not always what it looks from outside..
rectangles and squares can do wonders... :P
Nishant Bhaiya look here which is r8 before tiit war 1 broke out :P
 1
1NISHANT BHAIYA ... plz....GIVE SOME EXPLANATION......
OTHERWISE CAN U TELL ME OR POST ME HOW TO MAKE WEBSITES AND HOW DU U
ARRANGE FOR IT MY ID : mkagenius@gmail.com
 1
1i think mine is correct;
one more reason:
=========
UR LHS IS INTEGRATION OF FUNCTIONS ;
BUT RHS IS ONLY ADDITION AND SUBTRACTION OF RECTANGULAR AREAS;
HOW CAN THIS B POSSIBLE.
POINT OUT IF I 'M MISSING ANY POINT....
 33
33:D
pink is removed...
but which one is right...
i vote for mine :) thats why i designed my post ... [1]
 1
1nishant bhaiya...
u have pinked both of ours post ,
adding the two gives: 2∫f-1(x)dx=4af(b)-bf(a)-bf(b).
now u will pink this 1 too...i guess
 33
33Checked that for y=(x-2)2 from 1 to 2.......
 33
33checked it....
thats what i am getting.
May be i have got a mind block in this...
u try with a simple example ...
[1]
 1
1af(b) has no significance in sum of LHS.
But in the RHS it does not get cancelled.
 1
1i think thats incorrect.
can u check it again....
 33
33yes doing frm basic in such quesions is far better but then also..
i am getting this for f'(x)<0
f(a)∫f(b) f-1(x) dx +a∫b f(x) dx = 4af(b)-bf(a)-af(a)
 11
11Will the fact that the functions are inverses of each other help?
 33
33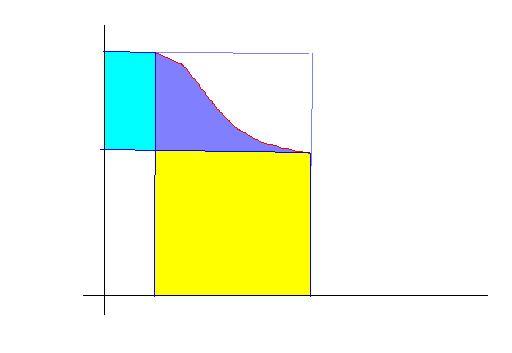
purple area is added twice when ∫f(x)+∫f-1(x)
:)
 33
33But i got some thing by drawing the fig.. :(
Ok let me recheck it..
:)
 341
341ya sorry. the limits are f(a) and f(b). But i dont get what the sign of f'(x) has got to do with it?
 33
33â–’â–‘â–’â–‘â–’â–‘â–’â–‘â–’â–‘â–’â–‘â–’â–‘â–’â–‘â–’â–‘â–’â–‘â–’â–‘â–’â–‘â–’â–‘â–’â–‘â–’â–‘â–’â–‘â–’â–‘â–’â–‘â–’â–‘
Plz check it..
for f'(x)≤0 where f'(x)=0 at discrete points..
f(a)∫f(b) f-1(x) dx +a∫b f(x) dx = 4af(b)-bf(a)-af(a)
b>a
â–’â–‘â–’â–‘â–’â–‘â–’â–‘â–’â–‘â–’â–‘â–’â–‘â–’â–‘â–’â–‘â–’â–‘â–’â–‘â–’â–‘â–’â–‘â–’â–‘â–’â–‘â–’â–‘â–’â–‘â–’â–‘â–’
 33
33But it should be this naa? may be a typing error...
f(a)∫f(b) f-1(x) dx +a∫b f(x) dx = b f(b) - a f(a)
for f'(x)≥0... where f'(x)=0 at discrete points and for f'(x)≤0 i think it should be different.. i am trying that..
[1]
 33
33a∫b f-1(x) dx +a∫b f(x) dx = b f(b) - a f(a)
is true for f'(x)≥0... [7]
 1
1all the things wat da above ppl. hav said is correct!!!
BUt i did it this way
assume √lnx as t;
U'll c dat on simplifcatn it turns out 2 b same as 1∫2 e^x2 dx
correct me if i'm wrong
 341
341Analytically you can use this result
a∫b f-1(x) dx +a∫b f(x) dx = b f(b) - a f(a)
Proof: In the first integral let x = f(t). Then f-1 f(x) = t
and dx = f'(t) dt
So now the integral is
a∫b tf'(t) dt + a∫b f(t) dt
= |tf(t)|ab - a∫b f(t) dt+a∫b f(t) dt
=bf(b) - a f(a)
So, now its easy to see that the answer is 2e4-e-a
 62
62I think this is correct...
Good work
AA=2e4 is the area from origin to the furthermost point
AB=e is the area of the origin to the first(closest) point
Then there is A1=a
A2 we need to find...
AA=AB+A1+A2
The figure below is for a general graph and not for this particular function....
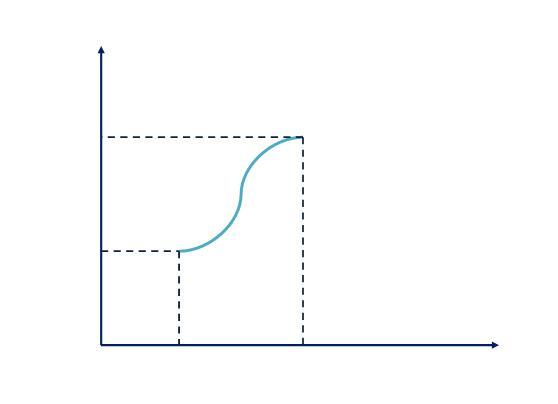
 62
62aragon it will matter a lot..
if you could think this far.. then you should be able to nail this one.... :)
 33
33First try with simpler functions..
may be..

