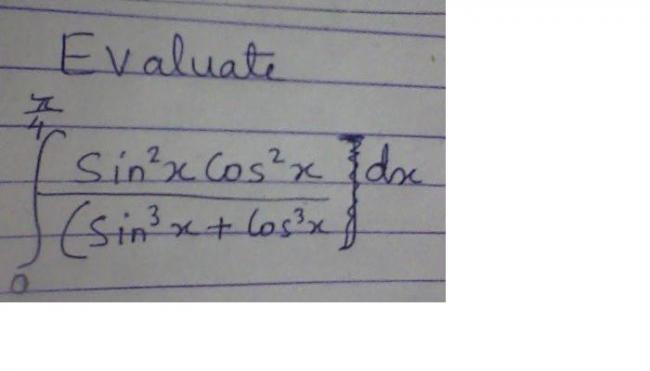Evaluate..

1 Answers

The integral is basically \int_{0}^{\frac{\pi}{4}}\frac{cos2x\sqrt{1-sin2x}}{2-sin2x}dx=\int_{0}^{\frac{\pi}{4}}\frac{sin2x\sqrt{1-cos2x}}{2-cos2x}dx

Take cos²x=k, from which we have l.\int_{\frac{1}{2}}^{1}{\frac{\sqrt{2k-1}}{2k}dk}

Where l is a const.

Now it is easy...

√ √ || {} [] () → ~ ^ x x x → → ln log lg lim lim cos sin tan cot arcsin arccos arctan

∫ ∫ ∫ ∫ ∫ ∬ ∬ ∬ ∬ ∬ ∭ ∭ ∭ ∭ ∭ ⨌ ⨌ ⨌ ⨌ ⨌

∑ ∑ ∑ ∑ ∑ ∮ ∮ ∮ ∮ ∮ ∏ ∏ ∏ ∏ ∏ ∐ ∐ ∐ ∐ ∐

+ - × ÷ ± ∓ = ∪ ∩ ≠ ∼ ≈ ∅ ∀ ∃ ∈ ∋ ∝ ≤ ≥ ≃ ≅ ≡ < > ≪ ≫ ⊂ ∉ ⊃ ⊆ ⊇ ⇒ ⇐ ⇔ ⇒ ⇐ ⇔ ⇑ ⇓ ⇕ → ← ↔ → ← ↔ ↑ ↓ ↕ ↖ ↗ ↘ ↙ ↪ ↩ ⇀ ↼ ⇁ ↽

° ∂ ∞ α β γ δ θ λ μ ν ξ π ρ σ φ ω ε ƒ κ τ υ Γ Δ Λ Σ Π Ω