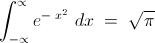
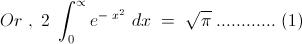
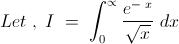
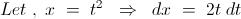
From ( 1 ) , we have : -
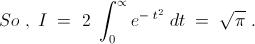
Given that
\int_{-\infty}^{\infty} e^{-x^2}\ \mathrm dx=\sqrt{\pi}
evaluate the integral
I=\int_0^\infty \dfrac{1}{\sqrt{x}}\ e^{-x}\ \mathrm dx
Please Explain the first step ( ... Eqn (i) ) that wherefrom that 2 came. Rest is OK.
Let I = - a ∫ a f ( x ) dx = - a ∫ 0 f ( x ) dx + 0 ∫ a f ( x ) dx
Let J = - a ∫ 0 f ( x ) dx
Let " x = - z " → " dx = - dz "
So , J = 0 ∫ a f ( - x ) dx .......... Since , - a ∫ 0 - f ( - z ) dz = 0 ∫ a f ( - z ) dz
Hence , I = 0 ∫ a f ( - x ) dx + 0 ∫ a f ( x ) dx
If " f " is an even function , then , " f ( - x ) = f ( x ) " .
Then , " I " would be = 2 0 ∫ a f ( x ) dx
Here , " e - x 2 " is an even function .
Hence , the result .
@vivek, if, f(x) = f(-x)
then, -a∫a f(x) dx =2 0∫a f(x).
here f(x) = f(-x).