13substitute( 1-x^a)^(1/b) = t
A strong candidate for JEE 2009!!
Find \int_0^1 (1-x^{2008})^{\frac{1}{2009}} dx - \int_0^1 (1-x^{2009})^{\frac{1}{2008}} dx
-
UP 0 DOWN 0 1 28
28 Answers
1When we substitute something in place of x should we not change the limits too??
that's what has been done.
13in 7 th last line limits of the second integral are 1 to 0 and then in the 3 rd last line they hav becum 0 to 1 without ny change in sign
1I can't see where you got that generalization.
that is not true.
But this one is: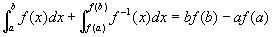
btw also see that I have not flipped the limits. I have substituted something in place of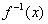 
....hope you will get my point .
21Lovely solution mate!!
OH K so v hav a generalization here :
∫f(x) + f-1(x) dx
xf-1(x)
EXPERTS PL. reply to this :
POST #10
13i didnt get the third last step ....
limits flip ho gayi but where is the minus sign.....
341jishnu can be recognized anywhere with his lucid posts. Good job bro
13integral xdx from 0 to 1 = integral tdt from 0 to 1...
hence after the above substitution v get the result....
1hmm..........thininkin.........[12]
thought of trying to take x 2009 out from one and x2008 from other but.............
21for the first integral :
I hav a feelin,
substitutin either 1-x2008 OR x2008 as sinθ cud b helpful
341In general we will have\int_0^1 (1-x^a)^{\frac{1}{b}} dx = \int_0^1 (1-x^b)^{\frac{1}{a}} dx
13sir will it b 0 for small constants like 1,2 or 3.... also
21Sir,
Nothing is for sure, but going by the ODDS, is my following observation likely 2b true than false :
wenever in integration, power/number as big as 2008/09 cums I hav a feeling dat the solution to such a problem cud b arrived at by treating the no. as any arbitrary constant a,
Now observing the relation b/w the BIG constant and other equally big const. (if any)
A GENERAL equation can b formed and then very simple values like 1,2 can b substituted!!!
21VERY BAD METHOD : [2]
this integral can b written as : (1 - xa)1/a+1 - (1 - xa+1)1/a
NOW let a = 1;
u wud find I = 0,
this generalsition cud b disastrous!! LAST option if nothin strikes
but this is a very crude methd & I mite get a beating frm math lovers here....
341Such problems will usually have a guessable answer. Here its ZERO
21I m tryin to solv dis one in the normal fashion, but Sir can u pl. provide us wid OPTIONS, coz I had a slite keyhole in mind by which v can judge the crrct option!!!
13the powers are so large .... and v hav 2 integrate only for numbers in 0 to 1....