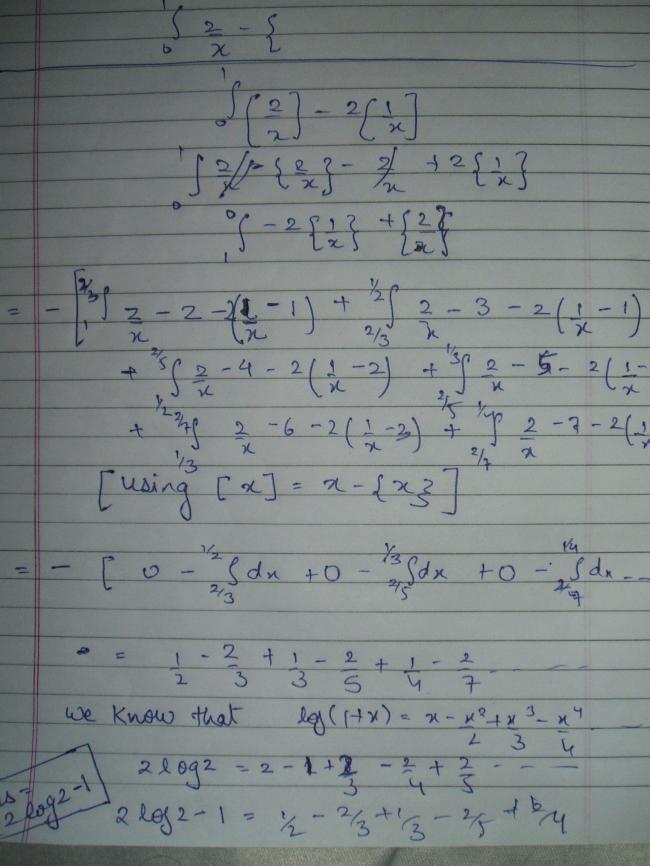i wud be glad to know abt some shorter method if u have it....
Evaluate:
\lim_{n\to\infty}\dfrac{1}{n}\sum_{k=1}^n\left(\left[\dfrac{2n}{k}\right]-2\left[\dfrac{n}{k}\right]\right)
Here [x] represents the greatest integer less than or equal to .
-
UP 0 DOWN 0 4 39

39 Answers
if all the mind is gone nuts then follow trapezoidal rule !
i felt since it is step fuction curve calculation would be easy..... is the answer +2 ????????
Skygirl, the answer you have obtained is not correct. Indeed, you can see the trouble since the integration of a everywhere positive integrand (can you prove it?) has turned out to be negative. The problem lies in you evaluation of the two integrals. The series you have obtained does not converges, neither does the second one. You cannot subtract two divergent series like usual numbers. And NO, the answer is not +2.
matlab the mystery is not solved yet[12][1]
THEN LETS SOLVE IT[4]
SIR PEHLE TELL ME IS THIS CORRECT
SO THAT I MAY PROCEED FURTHER

SORRY FOR GANDI WRITING
Kamyant Sir, if I could post something on this question started by you...
Well SkyGirl did most of the hard work that was there.. infact a lot of it... just that at this stage "Convergence" is not something that is easy to understand and to be fair it happens to be a topic of higher mathematics and not expected from JEE aspirants.
Having said that.. the only slight mistake in sky's solution is that she has taken incorrect intervals..
If she clubbed the intervals together, I think she would have got the answer...
Manipal.. and others if you can follow closely sky's solution adn try to find the answer?
@ manipal.. think ln(1+x) i think these could help
@kamyant sir: is the answer something like ln2-1?
Yes Nishant sir, I am aware that the issue of convergence is not in the JEE syllabus. However, I was just trying to point out why Skygirl was getting a negative value for something which is positive. Evaluated separately I1-I2 is something like ∞ - ∞ which is an indeterminate form.
Actually the answer is 2ln2 -1.
what i am just able to see that it should be between [-1,2].... post 7
[4]
answer is between that range.. my tukka was right...
Sir, even i tried this one and got the same answer what the Skygirl got. But what's wrong with that method. we are integating bitwin that limits wherein the [] func. has same value. indeed it must be correct !
I2 = \int_{0}^{1}{\left[\frac{1}{x} \right]dx}
=>I2 = \int_{1/2}^{1}{1. dx}+ \int_{1/3}^{1/2}{2. dx} + \int_{1/4}^{1/3}{3. dx}+ ...
=> I2 = 1.(1-1/2) + 2(1/2 - 1/3) + 3(1/3 - 1/4) + ....
now,
2X I2 = 2.(1-1/2) + 4(1/2 - 1/3) + 6(1/3 - 1/4) + .... = 2-1 +2+2+2....-(4/3+3/2+8/5+....)
so finally,
I1 - I2 = -1 . [am i correct bhaiya?]
\int_{1/n}^{1/n-1}\left\{{\left[ \frac{2}{x} \right]}-2{\left[ \frac{1}{x} \right]} \right\}dx
\\ =\int_{1/n}^{1/n-0.5}\left\{{\left[ \frac{2}{x} \right]}-2{\left[ \frac{1}{x} \right]} \right\}dx + \int_{1/n-0.5}^{1/n-1}\left\{{\left[ \frac{2}{x} \right]}-2{\left[ \frac{1}{x} \right]} \right\}dx
Now try this manipal :)
I dontwant topost the complete solution because this is meant for you guys and not for me...
If none of you do then may be Kamyant sir will postthe complete solution :)
thanks for the help
clue was needy
now i got the clue and will try to find the answer
@anand sir
i thoroughly want to thank u fro the bottom of my heart 4 creating this treasurous question
it was solved after a prolonged disscussion of 1:30 hours with KARANVEER (profile no.2132) [my classmate]
This is 1 of the best questions i ever faced in mathematics
and thanks to nishant sir 4 supporting throughout
no ur ans is wrong .....it is -1 those series will gt cancelled out
@deepanshu
I TRIED THE BEST I COULD DO 4 THIS QUESTION
I AGREE THAT IN THE LAST I WAS UNABLE TO JUSTIFY MY WORK DUE TO LESS SPACE
IF U HAVE DOUBTS I WILL CLEAR THEM
IF U THINK SOLUTION IS WRONG THEN I WILL BE GLAD TO SEE UR SOLUTION[1]
Let us convert the given problem into a " evaluation of a definite integral " problem .
We require to evaluate - I = 0∫1 { [ 2x ] - 2 [ 1x ] } dx
Let " f ( x ) = [ 2x ] - 2 [ 1x ]
Let us finish the problem by evaluating the area under the graph under the curve " y = f ( x ) " .
It is easy to see ( by sketching a graph ) that , for each number " n " , we have
f ( x ) = 0 ............for x E { ( 22 n + 1 , 22 n ] }
= 1 ........... for x E { ( 22 n + 2 , 22 n + 1 ] }
Therefore , I = ( 23 - 24 ) + ( 25 - 26 ) + ( 27 - 28 ) + .........= 2 ln 2 - 1
Grouping of similar terms is valid here since the series converges .
u must have seen him if u were there
one of the best members there
what i am just able to see that it should be between [-1,2] but don't know how good is my instinct on this... or am I talking a whole bit of nonsense....:P
aaege sochte hain....[12]