for all u iitians out there-even my fiitjee sir couldnt do this one

x=tan@^1/8]
dx=1/8 tan@^-7/8d@

1/8 ∫1tan^7/8@sec²@d@

1/8∫cos^23/8@sin^7/8@ d@

sin^7/8@=p
sin@=p^8/7

cos@=√1-p^16/7

7/8 sin^7/8cos^-1/8d@=dp

multiply numerator and denominator by cos^1/8@ sin^7/8@

1/8 ∫cos^1/8@ sin^7/8@cos^1/8@ sin^7/8@ cos^23/8@sin^7/8@ d@

= ∫(1-p^16/7)^3/2dp7p²

=∫1-p^24/77p²dp

=1/7∫ (dp/p²-p^24/7dp/p²

=1/7(-1/p-∫p^10/7dp

=-1/7(p + 7p^17/7/17)
ab p ki values daal do!!!!!!!!!

the solution is wrong-
the second step itself
if x=tan@^(1/8)
then by chain rule
dx=1/8 tan@^(7/8)(sec@^2)d@
---------------------------------------------------------

I don't know why you guys are so obsessed with indefinite integrals. One can easily see that
the function
F(x)= \int_1^x\dfrac{\mathrm dt}{1+t^{16}}
is an antiderivative, since
F^\prime(x)= \dfrac{1}{1+x^{16}}
As such the indefinite integral is easily obtained.

However, I understand that you are looking for some "actual" integral. So here it goes. You must note first that rational functions are one class of integrals which can always be represented in terms of elementary functions. The first thing to do is to break the rational function in to partial fractions.
The roots of x^{16}+1=0
are the 16th roots of -1. They are
x_k = e^{i\frac{(2k+1)\pi}{16}}, k = 0, 1, 2, ..., 15
As such
x^{16}+1=\prod_{k=0}^{15}(x-x_k)
Now we note that for each k from 0 to 7, the numbers x_k and x_15-k are conjugate to each other, since
x_kx_{15-k}=e^{i\frac{2k+1+2(15-k)+1}{16}\pi}=e^{2\pi i}=1
Hence,
x^{16}+1=\prod_{k=0}^{7}(x-x_k)(x_{15-k})=\prod_{k=0}^{7}(x^2-(x_k+x_{15-k})x+x_kx_{15-k})
But, x_k+x_{15-k}=x_k+\overline{x}_k=2\mathrm{Re}(x_k)=2\cos\dfrac{(2k+1)\pi}{16}
and x_kx_{15-k}=x_k\overline{x}_k=1
As such we get
1+x^{16}=\prod_{k=0}^7\left(x^2-2x\cos\frac{(2k+1)\pi}{16}+1\right)
Next, break 1x¹⁶+1 in to partial fraction. Then we shall have 8 terms which will be of the form
\dfrac{A_kx+B_k}{x^2-2x\cos\frac{(2k+1)\pi}{16}+1}
where the coefficients A_k and B_k have to be determined.
The point is that once you get this you could easily integrate each of the factors. Overall you will have to perform sixteen integration out of which 8 will come out as logarithm while the remaining 8 will be in terms of tan^-1.

After a long calculation (which I don't have the patience to write down), you will obtain
\int\dfrac{\mathrm dx}{1+x^{16}}=-\dfrac{1}{16}\sum_{k=0}^7\cos\frac{(2k+1)\pi}{16} \ln\left|x^2-2x\cos\frac{(2k+1)\pi}{16}+1\right|
+\dfrac{1}{8}\sum_{k=0}^7\sin\frac{(2k+1)\pi}{16}\tan^{-1}\left(\csc\frac{(2k+1)\pi}{16}\left\{x-\cos\frac{(2k+1)\pi}{16}\right\}\right) + C

(sry that post got bymistakely deleted , so posting it again )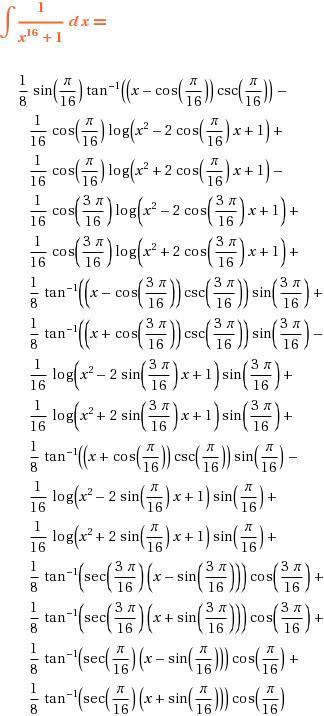

actually i found it from goiit ...hehe ...some one might hav copied it from mathematica as kaymant sir said , by the way i just posted it so that others may hav a feel of the answer .......... and aise bade ans ko dekh kar kaisi feelin aaegi wo bataneki zarurat bhi nahi hai [3]