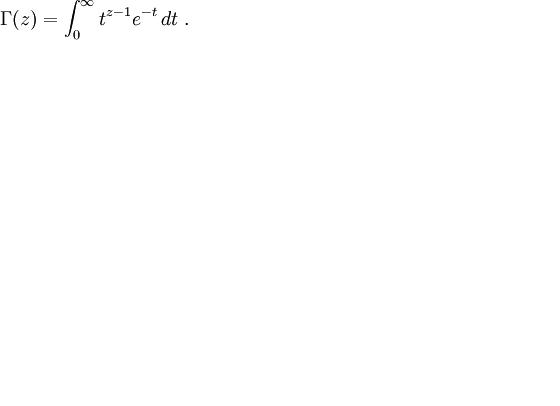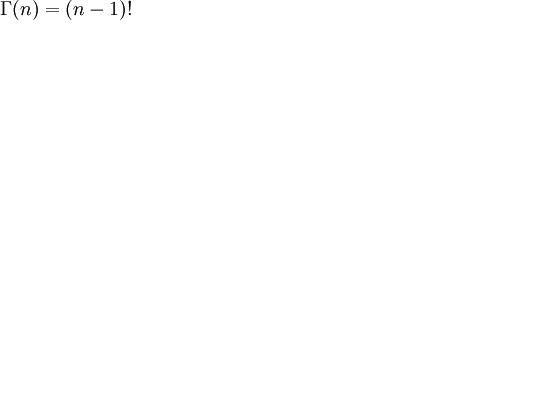GAMMA FUNCTION.....

In mathematics, the Gamma function (represented by the capitalized Greek letter Γ) is an extension of the factorial function to real and complex numbers. For a complex number z with positive real part the Gamma function is defined by

This definition can be extended to the rest of the complex plane, excepting the non-positive integers.

If n is a positive integer, then

showing the connection to the factorial function. The Gamma function generalizes the factorial function for non-integer and complex values of n.

The Gamma function is a component in various probability-distribution functions, and as such it is applicable in the fields of probability and statistics, as well as combinatorics.