1r des ur doubts [1] or jus posted for oders for practice
Q1 \int_{0}^{[x]/3}{\frac{8^x}{2^{[3x]}}}dx where [.] is gint
Q2 k ε N and I_k=\int_{-2k\pi}^{2k\pi}{\left|\sin x \right|}[\sin x]dx
find \sum_{k=1}^{100}I_k
Q3 I=\int_{sin^{-1}\alpha}^{cos^{-1}\alpha}{\frac {sinx}{sinx+cosx}}dx;\left| \alpha \right|\leq 1 ,find range of I
-
UP 0 DOWN 0 0 5
5 Answers
11Ans 2)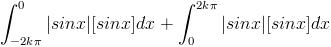 
=
=
=
=
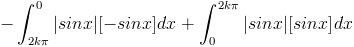
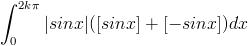
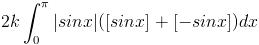
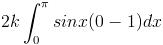
= -2k (- cosx) ................................;limits frm 0 to pie [bcoz sinx > 0 for x belonging to (0 , pie) ,
and - sinx < 0 for x belonging to (0, pie) ]
= -4k
Therefore,
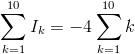= -4 . 10 . 112 = -220
11Ans 3)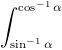 
sinxsinx + cosx dx
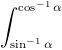= cosxsinx + cosx dx
[bcoz sin-1 x + cos -1x = pie/2]
On adding, we get
2 I = 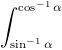1 . dx =
= 
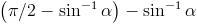
Therefore, I =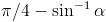 
Since,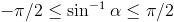 
Thereofre, Renge of I :- [-pie/4 , 3 pie/4]