if we consider
a^n/n!
then with each increasing value of n
a^n/n!
decreases by factor of a/n+1 of the previus term
now for any value of a if n>4 the value of a^n/n! becomes less than 1
(u change check that by taking any arbitrary value of a)
so if n→infinity
a^n/n! is less than 0
and hence tends to 0 in the neighbourhood
Find \lim_{n\rightarrow \infty}{\frac{a^n}{n!}}
I have this soln available with me..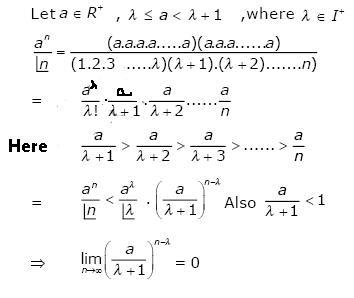
plz provide a new shorter soln..or help me to understand this soln..
-
UP 0 DOWN 0 0 8

8 Answers
yes thats what has been done but in a other way......just to make it look difficult to students.........
Let tn=an/n!
tn+1/tn = a/(n+1)
when n goes to infinity, this ratio goes to zero...
Hence, the limit is zero :)
if tn→0
then tn+1 must also →0
so can we have this tn+1/ tn ????
isnt it of 0/0 form ??
Or am I acting like a fooool :P
lol.. no no
see we dont have to find tn+1/ tn
What i have tried to do is to find this limit..
Thus, no matter what the value of tn be,
tn+1=tn × tn+1/tn
In a very stupid way to explain:
if the limit exists, tn will be finite.. and tn+1 will be zero times tn
In general note that for large positive integer n,
log n < xn < an < n!
That is the factorial increases faster than the exponential which in turn increases than the power function while the logarithm is the slowest among all.