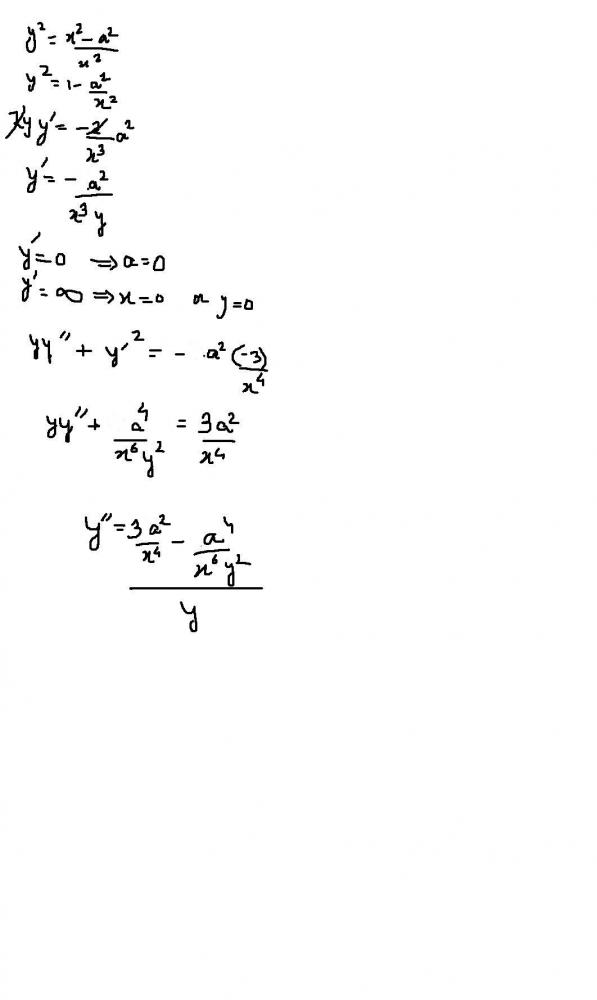would somebody like to answer to #16????
34 Answers
Q2
equation given: y2=x2-a2/x2
so x=0 ie y axis is obviously one asymptote
rewriting the equation in terms of x : x2=a2/1-y2
so y=±1 are asmptotes
so in total three asymptotes
Q1
when x=1 the y→∞ is easily observed from the equation
plotting not necessary for both the curves
that is all very deep manipal (ill try)
but the problem is simple enough without bringing in graphs
asymptotes can be found without graphs
i agree with ur method but please answer this 1
solve this 1
if
x2=102
so x will be equal to ????
ok.....but thanks to u........i had actually told to myself that i wont plot this.......but when u said that this plotting was out of our reach..then i got the inspiration and sudden burst of energy to solve this one...
arre why further discusson is going on on this topic???????
answer is 2 asymptotes......i checked in the answer key too..........
so dont worry .my soln is OK.....[1][1]
think properly..
here is definition of asymptote
An asymptote is a straight line at a finite distance from origin to which a given curve approaches indefinitely nearer as we recede towards infinite distance[1][1]
i agree wid u eureka...it wont touch in infinity
sir do u recognise the 2nd curve which is given in #1
can u help us with it????
x jab negative hoga to kya y bhi negative hoga[7][7][7]
r u sure about the 3rd and the 4th quadrants[12][12]
MAY BE 2ND ONE COULD BE BETTER EXPLAINED BY KAYMANT ,NISHANT OR PROPHET SIR
BECAUSE I HAD ASKED MY TEACHER TO FIND THE AREA UNDER THESE TYPE OF CURVES AND HE TOLD ME THAT THESE TYPE OF CURVES R STANDARD
THEY ALSO HAVE SOME NAMES 4 THEM
THEY READ ABOUT THESE THINGS IN THE ENGINEERING
it wont be that dificult .....
we have plotted descartes vala graph in graph of day.......
no they r not difficult but they r standard .
I wont say it is impossible to solve 4 us
But the actual thing in the question and its beauty could be explained by professionals better
so i leave this 1 4 them[1][108]
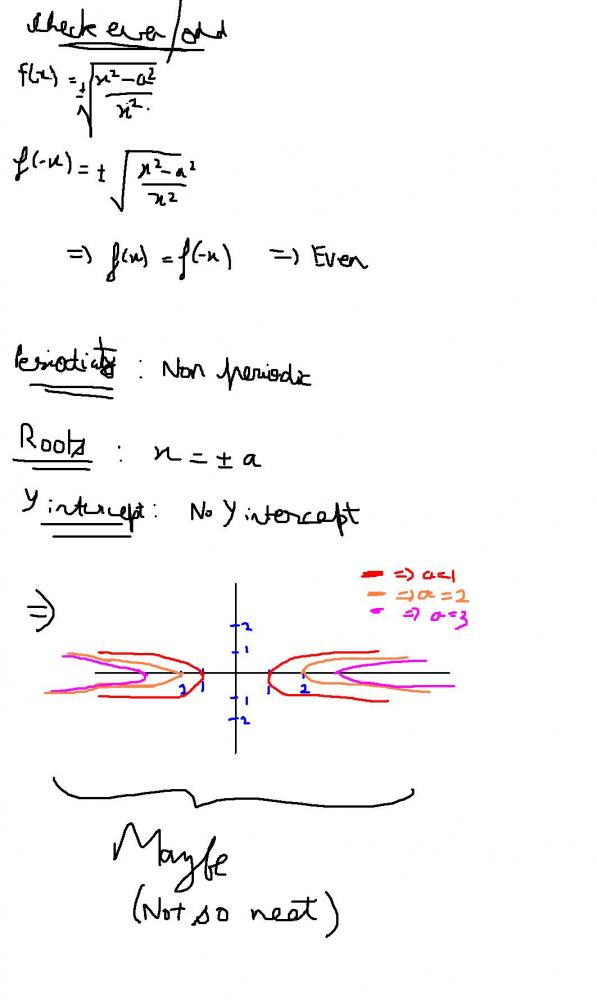
ok i am trying to plot 2nd one........
Domain
x2-a2≥0
&x≠0
=> x ε (-∞,-a]U[a,∞)
Range :
y2x2-x2+a2=0
=> x2(y2-1)+a2=0
since x real => D≥0
=> -4a2(y2-1)≥0
=>yε [-1,1]
range=> [-1,1]
i think u solved ur own problem
good use of algebra
but i was saying about the plotting thing..............