1bt i cant get a better method
& i m sure it cant be found using graph:(
32 Answers
1use f(f inv(x))=x
& differentiate & try to get ans
will post soln if req tmorw
1
33Yup thats what i wrote but it doesn't defines f-1(x) in terms of x.. but is only a equation which f-1(x) will satisfy
:)
33When u integrated it how u got that..
f-1(x)+sin(f-1(x))=x+C
:)
33No the answer is not right :P
See the range of your function and it should have been R for to be inverse of x+sinx
:)
1f(f inv(x))=x
d(f(f inv(x))/dx=1
so d(f inv(x))/dx=1/f'(f inv(x))
f'x=1+cosx
so f'(f inv(x))=1+cos(f inv(x))
d(f inv(x))/dx=1/1+cos(f inv(x))
(1+cos(f inv(x))d(f inv(x))=dx
integrate it
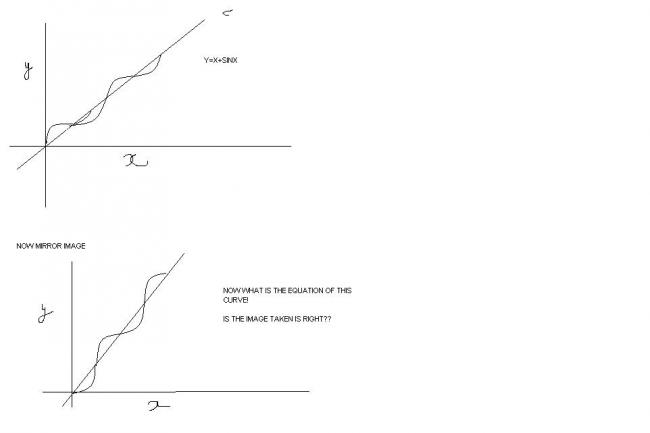
1NOW WHAT IS THE EQ OF THAT CURVE??
BY PRACTICALLY IT IS X-SINX.
1x-sinx is wrng
chk using f(f inv(x))=x
it jst resembles x-sinx acc to graph
1so how to do!
this question came in the test of BT papers!
and the answer given was x-sinx!
1sry bro i copied that frm abhi's post without thinking
also i hav tried the Q in our classroom conclusion was dat we cant solve it using graph
so plzz u better giv the s
1ya u could post the solution!
now i am in confusion f(f inv(x))=x or=1 or=0!!!!!!!
62well no paul and abhijeet and vishal.
The answer is not possible in closed form..
I think u can only do this one graphically :)
I will post the solution if u want!
But i want to see if..
if u see inverse function as (x-sinx)
then f(f-1(x)) = (x-sinx + sin(x-sinx)) which i dont see as 1 :)
1@abhi
dude cheak ma 1st post u cant find inv of x+sinx graphically
use f(f inv(x))=0
1by interchanging x & y!
the most probable answer is x-sinx!
but the problem is that f(f inverse(x))=0. iam not getting!
doen't it have to something with the symettry!
as it is symeetric about y=x so its inverse is same x+sinx!!!!!
1its not by taking x=y.
But by interchanging x & y axis graph of inverse is obtained.
1draw x+sinx graph then draw y=x graph then draw the image of x+sinx with respect to y=x and you will get it