if f(x) = [sin x + cos x] where 0< x < 2∩
[.] = greatest integer function
no. of points of discontinuity is
ans =5
how to go about???
if we draw the graph using ∩/4 as a unit and get the points of discontinuity
is this the correct method???
-
UP 0 DOWN 0 0 3
3 Answers
62best approach would be √2 (sin x + pi/4)
Then see where it becomes an integer...
49Is there any other approach that what u said to successfully solve the question?
1the graphical approach
from the graph of √2 (sin(x+π4))
we can draw the graph of
[√2 (sin(x+π4))]
the green color is the graph of
[√2 (sin(x+π4))]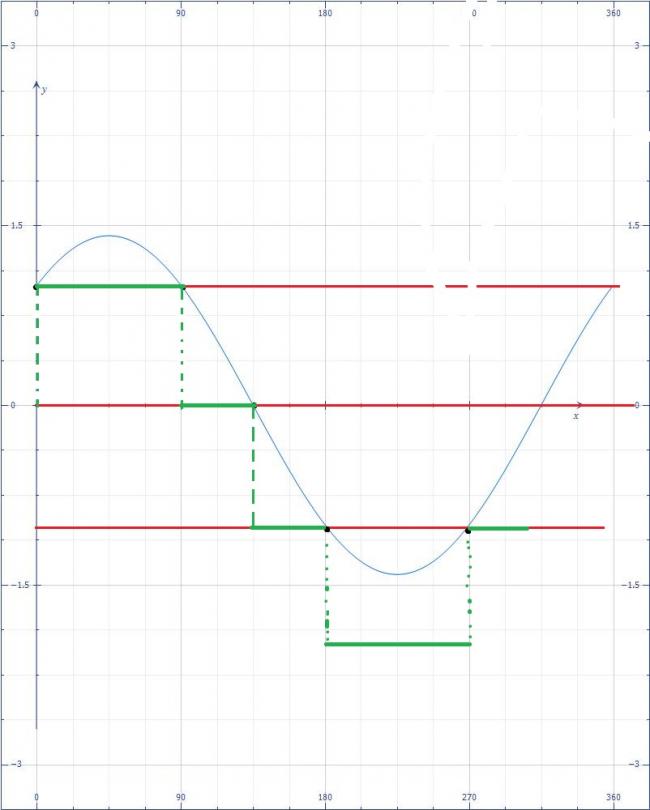
answer comes out to be 5
