g(x) would be f-1(x)
now i guess u will get ur answer
Suppose f(x)=(x+1)2 for x>=-1.If g(x) is the the function whose graph is the reflection of the graph of f(x) with respect to the line y=x,then g(x) equals
(a)-√x -1,x>=0
(b)1/(x+1)2,x>-1
(c)√x+1,x>=-1
(d)√x-1,x>=0
Please solve it in graphical and analytical method.
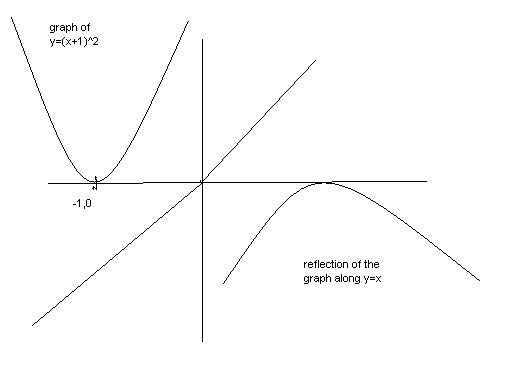
if i try to approach it in dis way can i get somewhere???
neglecting the points on left of (-1,0) .is this a correct approach??
see manmay's post..
What you are doing is wrong..
You have taken the mirror image about origin not the line y=x
bhaiya cud u please tell me y r we taking here inverse.seems dis is a sum of inverse of function.......
It is a property of all functions that across the line y = x, we get their inverses.
Suppose x and y are some input and output of a function on one side of y = x. The coordinate would be (x, y).
Symmetrically on the other side you will get (y, x) coordinate. This implies there is a function which gives F(y) = x. The only such function would be f-1(x).
The reason that they have given x ≥ -1 is to avoid problems to one-one and onto conditions. The function we have is one-one and onto or bijective as collectively called.
One-one means for a unique input x,the function gives a unique output y. There are no different inputs for one output.
Onto means that the range of the function matches its codomain(all possible values that can be obtained for values in the domain).
To find the inverse algebraically, you can use the property that fof-1(x) = x.
So here (f-1(x) + 1)² = x
Solve for f-1(x) as a quadratic and you'll get your answer.
There is another way to obtain the inverse of f(x) when its graph is given. Rotate the axes anti-clockwise by 90 degrees(alongwith the curve). Then take the mirror image of the axes and whatever curve is there(called flipping). You get the inverse function's graph. Try it.
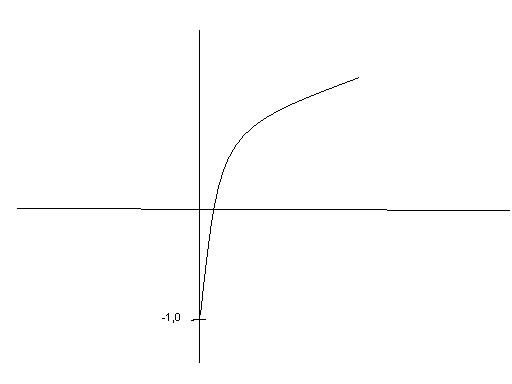
y=(x+1)2
x=√y-1
f-1(y)=√y-1
replacing y by x
we get
f-1(x)=√x-1
is dis wat we have to do pritsh bhaiya??
it is only to find the inverse,
let y = f(x) = (x+1)2 for x\geq -1
±√y = x+1 , x \geq -1
→ √y = x+1 → y \geq 0 , x+1\geq 0
→x = √y -1
f-1(y) = √y -1
→f-1(x) = √x -1 , x \geq 0